题目内容
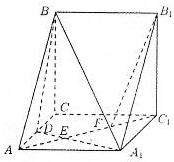 三棱柱ABC-A1B1C1中,CC1⊥平面ABC,D是AC的中点,A1D与AC1交于点E,F在线段AC1上,且AF=2FC1,AA1=1,AB=2,AC=1,∠BAC=60°.
三棱柱ABC-A1B1C1中,CC1⊥平面ABC,D是AC的中点,A1D与AC1交于点E,F在线段AC1上,且AF=2FC1,AA1=1,AB=2,AC=1,∠BAC=60°.(Ⅰ)求证:BC⊥平面AA1C1C;
(Ⅱ)求证:B1F∥平面A1BD;
(Ⅲ)求直线BC与平面A1BD所成的角的正弦值.
考点:直线与平面垂直的判定,直线与平面平行的判定,直线与平面所成的角
专题:证明题,空间位置关系与距离
分析:(Ⅰ)由CC1⊥平面ABC,BC⊆平面ABC,可证BC⊥CC1,在△ABC中,由余弦定理可证|AB|2=|BC|2+|AC|2,即有BC⊥AC,又AC⊆平面AA1CC1,CC1⊆平面AA1CC1,AC∩CC1=C,从而可证BC⊥平面AA1CC1.
(Ⅱ)以C为原点,分别以CA,CC1,CB所在直线为x轴,y轴,z轴建立空间直角坐标系O-xyz,则设F(x,y,0),由AF=2FC,可解得F,
坐标,令
=m
+n
,可解得存在m=1,n=
,使得
=m
+n
,可得向量
与
,
共面,又B1,F?平面A1BD,可证B1F∥平面A1BD.
(Ⅲ)由(Ⅱ)可求得
,
,
坐标,设平面A1BD的一个法向量m=(x,y,z),直线BC与平面A1BD所成的角为θ,由
,整理得
,令x=2
,求得平面A1BD的一个法向量m,从而由sinθ=|
|即可得解.
(Ⅱ)以C为原点,分别以CA,CC1,CB所在直线为x轴,y轴,z轴建立空间直角坐标系O-xyz,则设F(x,y,0),由AF=2FC,可解得F,
| FB |
| FB |
| DB |
| DA |
| 1 |
| 3 |
| FB |
| DB |
| DA |
| FB |
| DB |
| DA |
(Ⅲ)由(Ⅱ)可求得
| DB |
| DA1 |
| CB |
|
|
| 3 |
m•
| ||
| |m|•|CB| |
解答:
 解:(Ⅰ)∵CC1⊥平面ABC,BC⊆平面ABC,
解:(Ⅰ)∵CC1⊥平面ABC,BC⊆平面ABC,
∴BC⊥CC1,
在△ABC中,AB=2,AC=1,∠BAC=60°,
∴|BC|2=|AB|2+|AC|2-2|AB||AC|cos∠BAC=3,
则|AB|2=|BC|2+|AC|2,
∴∠BAC=90°,BC⊥AC,
又∵AC⊆平面AA1CC1,CC1⊆平面AA1CC1,AC∩CC1=C,
∴BC⊥平面AA1CC1.
(Ⅱ)由(Ⅰ)知CC1⊥CA,CC1⊥CB,AC⊥CB,
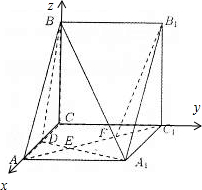
如图,以C为原点,分别以CA,CC1,CB所在直线为x轴,y轴,z轴建立空间直角坐标系O-xyz,则有A(1,0,0),B(0,0,
),A1(1,1,0),B1(0,1,
),C1(0,1,0),D(
,0,0),
设F(x,y,0),则
=(x-1,y,0),
=(-x,1-y,0),
∵AF=2FC,∴
,解得
,
即F(
,
,0),
=(-
,
,
),
若令
=m
+n
,可解得m=1,n=
,
∴存在m=1,n=
,使得
=m
+n
,
∴向量
与
,
共面,
又∵B1,F?平面A1BD,
∴B1F∥平面A1BD.
(Ⅲ)
=(-
,0,
),
=(
,1,0),
=(0,0,
),
设平面A1BD的一个法向量m=(x,y,z),直线BC与平面A1BD所成的角为θ,
由
得
,整理得
,
令x=2
,得平面A1BD的一个法向量m=(2
,-
,1),
所以sinθ=|
|=|
|=
.
故直线BC与与平面A1BD所成的角的正弦值为
.
 解:(Ⅰ)∵CC1⊥平面ABC,BC⊆平面ABC,
解:(Ⅰ)∵CC1⊥平面ABC,BC⊆平面ABC,∴BC⊥CC1,
在△ABC中,AB=2,AC=1,∠BAC=60°,
∴|BC|2=|AB|2+|AC|2-2|AB||AC|cos∠BAC=3,
则|AB|2=|BC|2+|AC|2,
∴∠BAC=90°,BC⊥AC,
又∵AC⊆平面AA1CC1,CC1⊆平面AA1CC1,AC∩CC1=C,
∴BC⊥平面AA1CC1.
(Ⅱ)由(Ⅰ)知CC1⊥CA,CC1⊥CB,AC⊥CB,
如图,以C为原点,分别以CA,CC1,CB所在直线为x轴,y轴,z轴建立空间直角坐标系O-xyz,则有A(1,0,0),B(0,0,
| 3 |
| 3 |
| 1 |
| 2 |
设F(x,y,0),则
| AF |
| FC |
∵AF=2FC,∴
|
|
即F(
| 1 |
| 3 |
| 2 |
| 3 |
| FB |
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
若令
| FB |
| DB |
| DA |
| 1 |
| 3 |
∴存在m=1,n=
| 1 |
| 3 |
| FB |
| DB |
| DA |
∴向量
| FB |
| DB |
| DA |
又∵B1,F?平面A1BD,
∴B1F∥平面A1BD.
(Ⅲ)
| DB |
| 1 |
| 2 |
| 3 |
| DA1 |
| 1 |
| 2 |
| CB |
| 3 |
设平面A1BD的一个法向量m=(x,y,z),直线BC与平面A1BD所成的角为θ,
由
|
|
|
令x=2
| 3 |
| 3 |
| 3 |
所以sinθ=|
m•
| ||
| |m|•|CB| |
| ||||
|
| 1 |
| 4 |
故直线BC与与平面A1BD所成的角的正弦值为
| 1 |
| 4 |
点评:本题考查直线与平面平行的证明,直线与平面垂直的判定,正确求出平面的法向量是解题的关键,解题时要认真审题,注意向量法的合理运用,考查了转化思想,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
二次函数y=x2+px+q的零点为1和m,且-1<m<0,那么p,q应满足的条件是( )
| A、p>0且p<0 |
| B、p>0且p>0 |
| C、p<0且p>0 |
| D、p<0且p<0 |
圆锥的母线长与底面半径所成的比为2:1,则该圆锥的侧面展开图中圆弧所对的圆心角为( )
A、
| ||
| B、π | ||
C、
| ||
D、
|
已知A,B,C三点共线,{an}为等差数列,且
=a2
+a12
,则a3+a15-a11的值为( )
| OC |
| OA |
| OB |
| A、1 | ||
| B、-1 | ||
C、
| ||
D、-
|
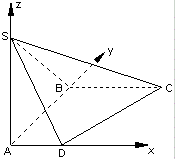 已知ABCD是直角梯形,∠ABC=90°,SA⊥平面ABCD,SA=AB=BC=1,AD=
已知ABCD是直角梯形,∠ABC=90°,SA⊥平面ABCD,SA=AB=BC=1,AD=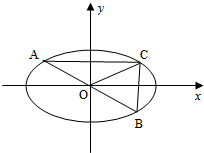 已知椭圆E:
已知椭圆E: