题目内容
二次函数y=x2+px+q的零点为1和m，且-1＜m＜0，那么p，q应满足的条件是（ ）
| A、p＞0且p＜0 |
| B、p＞0且p＞0 |
| C、p＜0且p＞0 |
| D、p＜0且p＜0 |
考点：函数的零点与方程根的关系
专题：函数的性质及应用
分析：利用二次函数的开口方向，零点的关系，列出不等式，推出结果即可．
解答：
解：二次函数y=x2+px+q，二次函数的开口向上，
两个零点为1和m，且-1＜m＜0，可得f（0）＜0，
可得q＜0，
又1+m＞0，
可得对称轴在y轴右侧．
即：-
＞0，
∴p＜0．
故选：D．
两个零点为1和m，且-1＜m＜0，可得f（0）＜0，
可得q＜0，
又1+m＞0，
可得对称轴在y轴右侧．
即：-
| p |
| 2 |
∴p＜0．
故选：D．
点评：本题考查函数的零点与方程的根的关系，二次函数的性质的应用，考查计算能力．
练习册系列答案
小学夺冠AB卷系列答案
相关题目
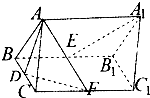如图，直三棱柱ABC-A1B1C1中，AB=AC=
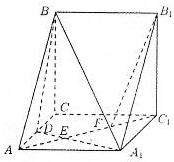三棱柱ABC-A1B1C1中，CC1⊥平面ABC，D是AC的中点，A1D与AC1交于点E，F在线段AC1上，且AF=2FC1，AA1=1，AB=2，AC=1，∠BAC=60°．圆锥的表面积公式（ ）
| A、S=πr2+πrl |
| B、S=2πr2+2πrl |
| C、S=πrl |
| D、S=πr2+πR2+πrl+πRl |