题目内容
试比较2n与n2(n∈N*)的大小关系,并用数学归纳法证明.
考点:数学归纳法
专题:综合题,点列、递归数列与数学归纳法
分析:利用数学归纳法证明,①易验证当n=5时不等式成立,②假设n=k(k≥5,k∈N*成立),利用该归纳假设,取推证当n=k+1时,不等式也成立即可.
解答:
解:当n=1时,2n=2,n2=1,2n>n2;
当n=2时,2n=4,n2=4,2n=n2;
当n=3时,2n=8,n2=9,2n<n2;
当n=4时,2n=16,n2=16,2n=n2;
当n=5时,2n=32,n2=25,2n>n2;
于是可猜测:2n>n2(n≥5).
证明:①当n=5时,均有2n>n2,不等式成立;
②假设n=k(k≥5,k∈N*)时不等式成立,即2k>k2;
则当n=k+1时,
左边=2k+1=2×2k>2k2,右边=(k+1)2=k2+2k+1,
∵k≥5,2k2-(k2+2k+1)=k2-2k-1=(k-1)2-2>0,
∴2k2>(k+1)2,
即当n=k+1时,2k+1>(k+1)2,不等式成立;
综上所述,2n>n2(n≥5,n∈N*).
当n=2时,2n=4,n2=4,2n=n2;
当n=3时,2n=8,n2=9,2n<n2;
当n=4时,2n=16,n2=16,2n=n2;
当n=5时,2n=32,n2=25,2n>n2;
于是可猜测:2n>n2(n≥5).
证明:①当n=5时,均有2n>n2,不等式成立;
②假设n=k(k≥5,k∈N*)时不等式成立,即2k>k2;
则当n=k+1时,
左边=2k+1=2×2k>2k2,右边=(k+1)2=k2+2k+1,
∵k≥5,2k2-(k2+2k+1)=k2-2k-1=(k-1)2-2>0,
∴2k2>(k+1)2,
即当n=k+1时,2k+1>(k+1)2,不等式成立;
综上所述,2n>n2(n≥5,n∈N*).
点评:本题考查数学归纳法,着重考查变形、推理与论证的能力,属于难题.

练习册系列答案
相关题目
圆锥的表面积公式( )
| A、S=πr2+πrl |
| B、S=2πr2+2πrl |
| C、S=πrl |
| D、S=πr2+πR2+πrl+πRl |
一个圆锥的表面积为π,它的侧面展开图是圆心角为120°的扇形,则该圆锥的高为( )
| A、1 | ||
B、
| ||
| C、2 | ||
D、2
|
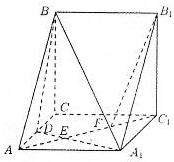 三棱柱ABC-A1B1C1中,CC1⊥平面ABC,D是AC的中点,A1D与AC1交于点E,F在线段AC1上,且AF=2FC1,AA1=1,AB=2,AC=1,∠BAC=60°.
三棱柱ABC-A1B1C1中,CC1⊥平面ABC,D是AC的中点,A1D与AC1交于点E,F在线段AC1上,且AF=2FC1,AA1=1,AB=2,AC=1,∠BAC=60°.