题目内容
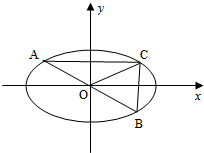 已知椭圆E:
已知椭圆E:| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 2 |
(Ⅰ)求椭圆E的方程;
(Ⅱ)若A,B,C是椭圆E上的三个动点,A,B关于原点对称,且△ABC的面积是4
| 2 |
考点:椭圆的简单性质
专题:方程思想,圆锥曲线的定义、性质与方程
分析:(Ⅰ)根据椭圆的离心率、椭圆过点(2,
)以及a2、b2、c2的关系,列出方程组,求出a2与b2即可;
(Ⅱ)由AB的直线方程与椭圆E的方程联立,求出|AB|的大小;再由OC的直线方程与椭圆E的方程联立,求出点C的坐标,
计算点C到直线AB的距离d,利用△ABC的面积求出k1k2的值.
| 2 |
(Ⅱ)由AB的直线方程与椭圆E的方程联立,求出|AB|的大小;再由OC的直线方程与椭圆E的方程联立,求出点C的坐标,
计算点C到直线AB的距离d,利用△ABC的面积求出k1k2的值.
解答:
解:(Ⅰ)根据题意,得;
椭圆E:
+
=1的离心率是
,
∴e=
=
①,
又椭圆E:
+
=1过点(2,
),
∴
+
=1②,
又∵a2=b2+c2③,
由①、②、③组成方程组,解得;
a2=8,b2=4;
∴椭圆E的方程为
+
=1;
(Ⅱ)根据题意,得;
AB所在直线方程为y=k1x,
代入椭圆E的方程并整理得:
(2k12+1)x2=8,
解得x=±
,
∴|AB|=
|x1-x2|=
•
;
又OC所在直线方程为:y=k2x,
与椭圆E的方程联立,得
;
解得C(±
,±
),
∴点C到直线AB的距离为d=
;
∴S△ABC=
|AB|•d=
=4
,
∴2k12-4k1k2+2k22=4k12k22+2k12+2k22+1,
∴4k12k22+4k1k2+1=0,
∴k1k2=-
.
椭圆E:
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
∴e=
| c |
| a |
| ||
| 2 |
又椭圆E:
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
∴
| 4 |
| a2 |
| 2 |
| b2 |
又∵a2=b2+c2③,
由①、②、③组成方程组,解得;
a2=8,b2=4;
∴椭圆E的方程为
| x2 |
| 8 |
| y2 |
| 4 |
(Ⅱ)根据题意,得;
AB所在直线方程为y=k1x,
代入椭圆E的方程并整理得:
(2k12+1)x2=8,
解得x=±
2
| ||
|
∴|AB|=
| 1+k12 |
| 1+k12 |
4
| ||
|
又OC所在直线方程为:y=k2x,
与椭圆E的方程联立,得
|
解得C(±
2
| ||
|
2
| ||
|
∴点C到直线AB的距离为d=
|
| ||||||
|
∴S△ABC=
| 1 |
| 2 |
| 8|k1-k2| | ||
|
| 2 |
∴2k12-4k1k2+2k22=4k12k22+2k12+2k22+1,
∴4k12k22+4k1k2+1=0,
∴k1k2=-
| 1 |
| 2 |
点评:本题考查了直线与椭圆方程的综合应用问题,也考查了方程组的解法与应用问题,点到直线的距离以及三角形面积的计算问题,是综合性题目.

练习册系列答案
相关题目
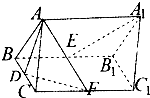 如图,直三棱柱ABC-A1B1C1中,AB=AC=
如图,直三棱柱ABC-A1B1C1中,AB=AC=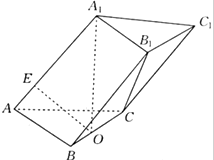 已知在三棱柱ABC-A1B1C1中,底面ABC为正三角形,A1在底面ABC上的射影是棱BC的中点O,OE⊥AA1于E点.
已知在三棱柱ABC-A1B1C1中,底面ABC为正三角形,A1在底面ABC上的射影是棱BC的中点O,OE⊥AA1于E点.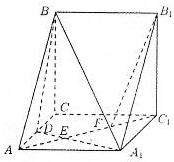 三棱柱ABC-A1B1C1中,CC1⊥平面ABC,D是AC的中点,A1D与AC1交于点E,F在线段AC1上,且AF=2FC1,AA1=1,AB=2,AC=1,∠BAC=60°.
三棱柱ABC-A1B1C1中,CC1⊥平面ABC,D是AC的中点,A1D与AC1交于点E,F在线段AC1上,且AF=2FC1,AA1=1,AB=2,AC=1,∠BAC=60°.