题目内容
已知A,B,C三点共线,{an}为等差数列,且
=a2
+a12
,则a3+a15-a11的值为( )
| OC |
| OA |
| OB |
| A、1 | ||
| B、-1 | ||
C、
| ||
D、-
|
考点:平面向量的基本定理及其意义,等差数列的通项公式
专题:平面向量及应用
分析:A,B,C三点共线,且
=a2
+a12
,利用向量共线定理可得:a2+a12=1.利用等差数列的性质可得a7=
.a3+a15-a11=a7,即可得出.
| OC |
| OA |
| OB |
| 1 |
| 2 |
解答:
解:∵A,B,C三点共线,且
=a2
+a12
,
∴a2+a12=1,
∵{an}为等差数列,
∴2a7=1,即a7=
.
则a3+a15-a11=a7=
.
故选:C.
| OC |
| OA |
| OB |
∴a2+a12=1,
∵{an}为等差数列,
∴2a7=1,即a7=
| 1 |
| 2 |
则a3+a15-a11=a7=
| 1 |
| 2 |
故选:C.
点评:本题考查了向量共线定理、平面向量基本定理、等差数列的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
母线长为1的圆锥的侧面展开图的圆心角为π,则这个圆锥的体积为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
圆锥的表面积公式( )
| A、S=πr2+πrl |
| B、S=2πr2+2πrl |
| C、S=πrl |
| D、S=πr2+πR2+πrl+πRl |
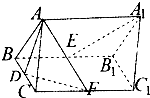 如图,直三棱柱ABC-A1B1C1中,AB=AC=
如图,直三棱柱ABC-A1B1C1中,AB=AC=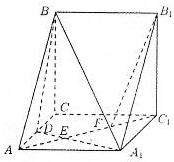 三棱柱ABC-A1B1C1中,CC1⊥平面ABC,D是AC的中点,A1D与AC1交于点E,F在线段AC1上,且AF=2FC1,AA1=1,AB=2,AC=1,∠BAC=60°.
三棱柱ABC-A1B1C1中,CC1⊥平面ABC,D是AC的中点,A1D与AC1交于点E,F在线段AC1上,且AF=2FC1,AA1=1,AB=2,AC=1,∠BAC=60°.