题目内容
已知函数f(x)=2sinxcosx-2cos2x-1.
(Ⅰ)求f(x)的最小正周期及对称轴方程;
(Ⅱ)求f(x)在区间[0,
]上的最大值.
(Ⅰ)求f(x)的最小正周期及对称轴方程;
(Ⅱ)求f(x)在区间[0,
| π |
| 2 |
考点:三角函数中的恒等变换应用,三角函数的周期性及其求法
专题:三角函数的求值,三角函数的图像与性质
分析:(Ⅰ)首先通过三角函数的恒等变换,把函数的关系式变形成正弦型函数,进一步求出函数的周期和对称轴方程.
(Ⅱ)直接利用函数的定义域,利用整体思想求正弦型函数的值域,进一步求出函数的最值.
(Ⅱ)直接利用函数的定义域,利用整体思想求正弦型函数的值域,进一步求出函数的最值.
解答:
解:(Ⅰ)f(x)=2sinxcosx-2cos2x-1
=sin2x-(cos2x+1)-1
=
sin(2x-
)-2.
所以:函数的最小正周期为:T=
=π
令:2x-
=kπ+
(k∈Z)
解得:x=
+
(k∈Z)
(Ⅱ)由于:0≤x≤
所以:-
≤2x-
≤
所以:-1≤
sin(2x-
)≤
进一步求得:-3≤f(x)≤
-2
所以:函数的最大值为:
-2
=sin2x-(cos2x+1)-1
=
| 2 |
| π |
| 4 |
所以:函数的最小正周期为:T=
| 2π |
| 2 |
令:2x-
| π |
| 4 |
| π |
| 2 |
解得:x=
| kπ |
| 2 |
| 3π |
| 8 |
(Ⅱ)由于:0≤x≤
| π |
| 2 |
所以:-
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
所以:-1≤
| 2 |
| π |
| 4 |
| 2 |
进一步求得:-3≤f(x)≤
| 2 |
所以:函数的最大值为:
| 2 |
点评:本题考查的知识要点:三角函数关系式的恒等变换,正弦型函数的性质的应用,周期性的应用,对称性的应用,利用函数的定义域求出函数的值域.属于基础题型.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
设函数f(x)=
x3+
ax2+2bx+c,f(x)在x=x1处取得极大值,在x=x2处取得极小值,且x1∈(0,1),x2∈(1,2),则
的取值范围为( )
| 1 |
| 3 |
| 1 |
| 2 |
| b-2 |
| a-1 |
| A、(1,4) | ||||
B、(
| ||||
C、(
| ||||
D、(
|
已知f(1)=1,f(x)=
(x=2,3,…),m∈N+,则f(2m)=( )
|
| A、2m+1 | |||||
B、
| |||||
C、
| |||||
| D、3m2+2m |
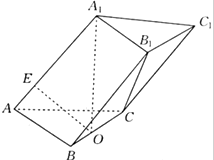 已知在三棱柱ABC-A1B1C1中,底面ABC为正三角形,A1在底面ABC上的射影是棱BC的中点O,OE⊥AA1于E点.
已知在三棱柱ABC-A1B1C1中,底面ABC为正三角形,A1在底面ABC上的射影是棱BC的中点O,OE⊥AA1于E点.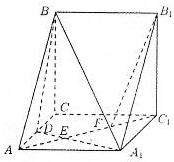 三棱柱ABC-A1B1C1中,CC1⊥平面ABC,D是AC的中点,A1D与AC1交于点E,F在线段AC1上,且AF=2FC1,AA1=1,AB=2,AC=1,∠BAC=60°.
三棱柱ABC-A1B1C1中,CC1⊥平面ABC,D是AC的中点,A1D与AC1交于点E,F在线段AC1上,且AF=2FC1,AA1=1,AB=2,AC=1,∠BAC=60°.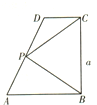 如图所示,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2,CD=1,BC=a(a>0),P为线段AD(含端点)上一个动点,设
如图所示,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2,CD=1,BC=a(a>0),P为线段AD(含端点)上一个动点,设