Question

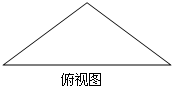一个底面是等腰直角三角形的直棱柱，侧棱长与底面三角形的腰长相等，其体积为4，它的三视图中俯视图如图所示，侧视图是一个矩形，则这个矩形的对角线长为

 

．

Answer 1

考点：简单空间图形的三视图

专题：计算题,空间位置关系与距离

分析：设底面等腰直角三角形的直角边长为x，由侧棱长与底面三角形的腰长相等，其体积为4，求得x，再求侧视图矩形的底边长与高，利用勾股定理求其对角线长．

解答： 解：设底面等腰直角三角形的直角边长为x，由侧棱长与底面三角形的腰长相等，其体积为4，
得

1

2

x³=4⇒x=2，∴棱柱的高为2，
侧视图是矩形，底边长为底面等腰直角三角形斜边上的高，
矩形的底边长为

2

，
∴矩形的对角线长为

22+2

=

6

．
故答案是

6

．

点评：本题考查几何体的三视图的应用，侧视图的面积的求法，考查计算能力．