题目内容
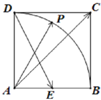 如图所示,在正方形ABCD中,E为AB的中点,P是以A为圆心,AB为半径的圆弧BD上的任意一点,设∠PAB=θ,向量
如图所示,在正方形ABCD中,E为AB的中点,P是以A为圆心,AB为半径的圆弧BD上的任意一点,设∠PAB=θ,向量| AC |
| DE |
| AP |
考点:向量加减混合运算及其几何意义
专题:平面向量及应用
分析:如图所示,建立直角坐标系.不妨设正方形ABCD的边长为1.则A(0,0),D(0,1),C(1,1),P(cosθ,sinθ),E(
,0).由于向量
=λ
+μ
(λ,μ∈R),又μ-λ=1,可得
=λ
+(1+λ)
,化为
=λ(
+
).再利用向量共线定理即可得出.
| 1 |
| 2 |
| AC |
| DE |
| AP |
| AC |
| DE |
| AP |
| PC |
| DE |
| AP |
解答:
解:如图所示,建立直角坐标系.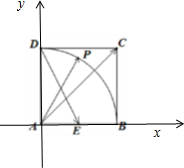
不妨设正方形ABCD的边长为1.
则A(0,0),D(0,1),C(1,1),P(cosθ,sinθ),E(
,0).
∴
=(1-cosθ,1-sinθ),
=(
,-1),
=(cosθ,sinθ).
+
=(
+cosθ,-1+sinθ).
∵向量
=λ
+μ
(λ,μ∈R),又μ-λ=1,
∴
=λ
+(1+λ)
,化为
=λ(
+
).
∴(1-cosθ)(-1+sinθ)-(1-sinθ)(
+cosθ)=0,
化为sinθ=1,
∵θ∈[0°,90°],∴θ=90°.
故答案为:90°.

不妨设正方形ABCD的边长为1.
则A(0,0),D(0,1),C(1,1),P(cosθ,sinθ),E(
| 1 |
| 2 |
∴
| PC |
| DE |
| 1 |
| 2 |
| AP |
| DE |
| AP |
| 1 |
| 2 |
∵向量
| AC |
| DE |
| AP |
∴
| AC |
| DE |
| AP |
| PC |
| DE |
| AP |
∴(1-cosθ)(-1+sinθ)-(1-sinθ)(
| 1 |
| 2 |
化为sinθ=1,
∵θ∈[0°,90°],∴θ=90°.
故答案为:90°.
点评:本题考查了向量的坐标运算和向量共线定理,属于基础题.

练习册系列答案
相关题目
若直线(a+2)x+(1-a)y=a2(a>0)与直线(a-1)x+(2a+3)y+2=0互相垂直,则a等于( )
| A、1 | B、-1 | C、±1 | D、-2 |
已知函数f(x)=
,则f(f(-π))的值等于( )
|
|
| A、π2-1或0 |
| B、π2-1 |
| C、0 |
| D、-π |
如图所示,程序框图的输出结果为( )


A、
| ||
B、
| ||
C、
| ||
D、
|
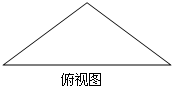 一个底面是等腰直角三角形的直棱柱,侧棱长与底面三角形的腰长相等,其体积为4,它的三视图中俯视图如图所示,侧视图是一个矩形,则这个矩形的对角线长为
一个底面是等腰直角三角形的直棱柱,侧棱长与底面三角形的腰长相等,其体积为4,它的三视图中俯视图如图所示,侧视图是一个矩形,则这个矩形的对角线长为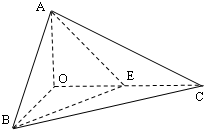 如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点.
如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点.