题目内容
以下是收集到的新房屋销售价格y与房屋的大小x的数据:
(1)画出数据的散点图;
(2)用最小二乘法估计求线性回归方程,并在散点图中加上回归直线.
| 房屋大小 x(m2) |
80 | 105 | 110 | 115 | 135 |
| 销售价格y(万元) | 18.4 | 22 | 21.6 | 24.8 | 29.2 |
(2)用最小二乘法估计求线性回归方程,并在散点图中加上回归直线.
考点:可线性化的回归分析
专题:计算题,应用题,概率与统计
分析:(1)根据表中所给的五对数据,在平面直角坐标系中描出这五个点,得到这组数据的散点图.
(2)根据表中所给的数据,求出横标和纵标的平均数,把求得的数据代入求线性回归方程的系数的公式,利用最小二乘法得到结果,写出线性回归方程.
(2)根据表中所给的数据,求出横标和纵标的平均数,把求得的数据代入求线性回归方程的系数的公式,利用最小二乘法得到结果,写出线性回归方程.
解答:
解:(1)数据对应的散点图如图所示:
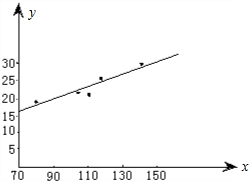
(2)n=5,
xi=545,
=109,
yi=116,
=23.2,
xi2=60952,
xiyi=12952,
b=
≈0.1962,a=23.2-0.1962×109≈1.8166,
所以,线性回归方程为y=0.1962x+1.8166.

(2)n=5,
| 5 |
 |
| i=1 |
. |
| x |
| 5 |
 |
| i=1 |
. |
| y |
| 5 |
 |
| i=1 |
| 5 |
 |
| i=1 |
b=
| 5×12952-545×116 |
| 5×60952-5452 |
所以,线性回归方程为y=0.1962x+1.8166.
点评:本题考查了线性回归方程的求法与应用,解答本题的关键是用最小二乘法求线性回归直线方程的系数,计算要细心.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
点P(2,3)到直线:ax+(a-1)y+3=0的距离d为最大时,d与a的值依次为( )
| A、3,-3 | B、5,1 |
| C、5,2 | D、7,1 |
已知tanα=-
,则sin2α-2cos2α-1=( )
| 1 |
| 2 |
A、-
| ||
B、-
| ||
C、-
| ||
| D、-2 |
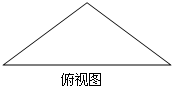 一个底面是等腰直角三角形的直棱柱,侧棱长与底面三角形的腰长相等,其体积为4,它的三视图中俯视图如图所示,侧视图是一个矩形,则这个矩形的对角线长为
一个底面是等腰直角三角形的直棱柱,侧棱长与底面三角形的腰长相等,其体积为4,它的三视图中俯视图如图所示,侧视图是一个矩形,则这个矩形的对角线长为