题目内容
已知直线x-my+3=0和圆x2+y2-6x+5=0,当圆被直线截得的弦长为
时,m= .
2
| ||
| 5 |
考点:直线与圆相交的性质
专题:直线与圆
分析:先求出圆的圆心,再由点到直线的距离公式求出圆心到直线的距离,再根据圆被直线截得的弦长,利用垂径定理能求出m的值.
解答:
解:把圆x2+y2-6x+5=0转化为标准方程,得(x-3)2+y2=4,
圆心(3,0)到直线x-my+3=0的距离d=
=
,
∵圆被直线截得的弦长为
,
∴由垂径定理,得:(
)2=4-(
)2,
解得m=±3.
故答案为:±3.
圆心(3,0)到直线x-my+3=0的距离d=
| |3+3| | ||
|
| 6 | ||
|
∵圆被直线截得的弦长为
2
| ||
| 5 |
∴由垂径定理,得:(
| ||
| 5 |
| 6 | ||
|
解得m=±3.
故答案为:±3.
点评:本题考查直线与圆的位置关系的应用,涉及到点到直线的距离公式、圆、垂径定理等知识点,是中档题.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目
若直线(a+2)x+(1-a)y=a2(a>0)与直线(a-1)x+(2a+3)y+2=0互相垂直,则a等于( )
| A、1 | B、-1 | C、±1 | D、-2 |
把89化这二进制数,其结果为( )
| A、1001101 |
| B、1100101 |
| C、1011011 |
| D、1011001 |
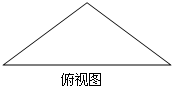 一个底面是等腰直角三角形的直棱柱,侧棱长与底面三角形的腰长相等,其体积为4,它的三视图中俯视图如图所示,侧视图是一个矩形,则这个矩形的对角线长为
一个底面是等腰直角三角形的直棱柱,侧棱长与底面三角形的腰长相等,其体积为4,它的三视图中俯视图如图所示,侧视图是一个矩形,则这个矩形的对角线长为