题目内容
3.已知数列{an}的前n项和为Sn,点(n,Sn)在函数f(x)=${∫}_{1}^{x}$(2t+1)dt的图象上,则数列{an}的通项公式为( )| A. | an=2n-2 | B. | an=n2+n-2 | ||
| C. | an=$\left\{\begin{array}{l}{0,}&{n=1}\\{2n-1,}&{n≥2}\end{array}\right.$ | D. | an=$\left\{\begin{array}{l}{0,}&{n=1}\\{2n,}&{n≥2}\end{array}\right.$ |
分析 通过计算可知${∫}_{1}^{x}$(2t+1)dt=x2+x-2,从而Sn=n2+n-2,当n≥2时利用an=Sn-Sn-1可知an=2n,进而计算可得结论.
解答 解:∵${∫}_{1}^{x}$(2t+1)dt=x2+x-2,
∴Sn=n2+n-2,
∴当n≥2时,an=Sn-Sn-1=2n,
又∵a1=S1=1+1-2=0不满足上式,
∴an=$\left\{\begin{array}{l}{0,}&{n=1}\\{2n,}&{n≥2}\end{array}\right.$,
故选:D.
点评 本题考查数列的通项,涉及定积分的计算,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
14.过抛物线y2=2px(p>0)的焦点F的直线交抛物线于A,B两点,点O是原点,如果|BF|=3,|BF|>|AF|,$∠BFO=\frac{2π}{3}$,那么|AF|的值为( )
| A. | 1 | B. | $\frac{3}{2}$ | C. | 3 | D. | 6 |
8.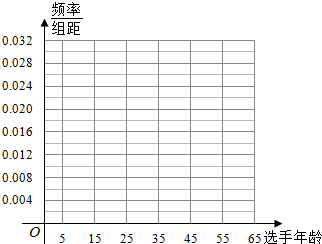 《中国梦想秀》是浙江卫士推出的一档“真人秀”综艺节目,节目开播至今,有上百组的追梦人在这个舞台上实现了自己的梦想,某机构随机抽取100名参与节目的选手,以他们的年龄作为样本进行分析研究,并根据所得数据作出如下频数分布表:
《中国梦想秀》是浙江卫士推出的一档“真人秀”综艺节目,节目开播至今,有上百组的追梦人在这个舞台上实现了自己的梦想,某机构随机抽取100名参与节目的选手,以他们的年龄作为样本进行分析研究,并根据所得数据作出如下频数分布表:
(Ⅰ)在表中作出这些数据的频率分布直方图;
(Ⅱ)已知样本中年龄在[55,65]内的6位选手中,有4名女选手,2名男选手,现从中选3人进行回访,记选出的女选手的人数为X,求X的分布列、数学期望与方差.
 《中国梦想秀》是浙江卫士推出的一档“真人秀”综艺节目,节目开播至今,有上百组的追梦人在这个舞台上实现了自己的梦想,某机构随机抽取100名参与节目的选手,以他们的年龄作为样本进行分析研究,并根据所得数据作出如下频数分布表:
《中国梦想秀》是浙江卫士推出的一档“真人秀”综艺节目,节目开播至今,有上百组的追梦人在这个舞台上实现了自己的梦想,某机构随机抽取100名参与节目的选手,以他们的年龄作为样本进行分析研究,并根据所得数据作出如下频数分布表:| 选手年龄 | [5,15) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65] |
| 频数 | 6 | 22 | 32 | 24 | 10 | 6 |
(Ⅱ)已知样本中年龄在[55,65]内的6位选手中,有4名女选手,2名男选手,现从中选3人进行回访,记选出的女选手的人数为X,求X的分布列、数学期望与方差.
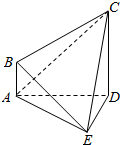 如图,在四棱锥E-ABCD中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=3AB.
如图,在四棱锥E-ABCD中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=3AB.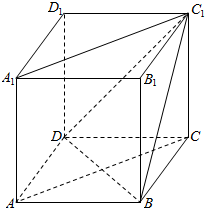 如图,在正方体ABCD-A1B1C1D1中,求直线BC1与AC的夹角60°.
如图,在正方体ABCD-A1B1C1D1中,求直线BC1与AC的夹角60°.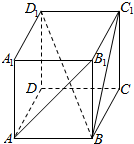 如图,在正方体ABCD-A1B1C1D1中.求:
如图,在正方体ABCD-A1B1C1D1中.求: