题目内容
15.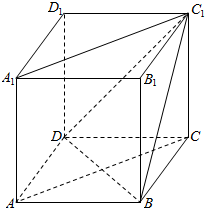 如图,在正方体ABCD-A1B1C1D1中,求直线BC1与AC的夹角60°.
如图,在正方体ABCD-A1B1C1D1中,求直线BC1与AC的夹角60°.
分析 由AC∥A1C1,得∠A1C1B是异面直线BC1与AC所成角,由此能求出直线BC1与AC的夹角.
解答 解:∵AC∥A1C1,
∴∠A1C1B是异面直线BC1与AC所成角,
∵A1C1=BC1=BD,
∴∠A1C1B=60°,
∴直线BC1与AC的夹角为60°.
故答案为:60°.
点评 本题考查异面直线所成角的求法,是基础题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
6. 某程序框图如图所示,当输入的x的值为5时,输出的y值恰好是$\frac{1}{3}$,则在空白的处理框处应填入的关系式可以是( )
某程序框图如图所示,当输入的x的值为5时,输出的y值恰好是$\frac{1}{3}$,则在空白的处理框处应填入的关系式可以是( )
 某程序框图如图所示,当输入的x的值为5时,输出的y值恰好是$\frac{1}{3}$,则在空白的处理框处应填入的关系式可以是( )
某程序框图如图所示,当输入的x的值为5时,输出的y值恰好是$\frac{1}{3}$,则在空白的处理框处应填入的关系式可以是( )| A. | y=x3 | B. | y=3x | C. | y=3x | D. | $y=\frac{3}{x}$ |
3.已知数列{an}的前n项和为Sn,点(n,Sn)在函数f(x)=${∫}_{1}^{x}$(2t+1)dt的图象上,则数列{an}的通项公式为( )
| A. | an=2n-2 | B. | an=n2+n-2 | ||
| C. | an=$\left\{\begin{array}{l}{0,}&{n=1}\\{2n-1,}&{n≥2}\end{array}\right.$ | D. | an=$\left\{\begin{array}{l}{0,}&{n=1}\\{2n,}&{n≥2}\end{array}\right.$ |
4. 已知P是双曲线$\frac{{x}^{2}}{3}$-y2=1上任意一点,过点P分别作曲线的两条渐近线的垂线,垂足分别为A、B,则$\overrightarrow{PA}$•$\overrightarrow{PB}$的值是( )
已知P是双曲线$\frac{{x}^{2}}{3}$-y2=1上任意一点,过点P分别作曲线的两条渐近线的垂线,垂足分别为A、B,则$\overrightarrow{PA}$•$\overrightarrow{PB}$的值是( )
 已知P是双曲线$\frac{{x}^{2}}{3}$-y2=1上任意一点,过点P分别作曲线的两条渐近线的垂线,垂足分别为A、B,则$\overrightarrow{PA}$•$\overrightarrow{PB}$的值是( )
已知P是双曲线$\frac{{x}^{2}}{3}$-y2=1上任意一点,过点P分别作曲线的两条渐近线的垂线,垂足分别为A、B,则$\overrightarrow{PA}$•$\overrightarrow{PB}$的值是( )| A. | -$\frac{3}{8}$ | B. | $\frac{3}{16}$ | C. | -$\frac{\sqrt{3}}{8}$ | D. | 不能确定 |
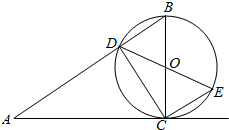 如图,BC是圆O的直径,过C作圆O的切线AC,连接AB交圆O于点D.
如图,BC是圆O的直径,过C作圆O的切线AC,连接AB交圆O于点D.