题目内容
已知定线段AB所在的直线与定平面α相交,P为直线AB外的一点,且P不在α内,若直线AP,BP与α分别交于C,D点,求证:不论P在什么位置,直线CD必过一定点.
考点:分析法和综合法
专题:空间位置关系与距离
分析:由已知中定线段AB所在的直线与定平面α相交,直线AP、BP与α分别交于C、D点,根据公理3可判断直线CD必过一定点.
解答:
证明:设定线段AB所在直线为l,与平面α交于O点,即l∩α=O.
由题意可知,AP∩α=C,BP∩α=D,∴C∈α,D∈α.
又∵AP∩BP=P.
∴AP、BP可确定一平面β且C∈β,D∈β.
∴CD=α∩β.∴A∈β,B∈β.∴l?β.∴O∈β.∴O∈α∩β,即O∈CD.
∴不论P在什么位置,直线CD必过一定点.
由题意可知,AP∩α=C,BP∩α=D,∴C∈α,D∈α.
又∵AP∩BP=P.
∴AP、BP可确定一平面β且C∈β,D∈β.
∴CD=α∩β.∴A∈β,B∈β.∴l?β.∴O∈β.∴O∈α∩β,即O∈CD.
∴不论P在什么位置,直线CD必过一定点.
点评:本题考查空间直线与直线的位置关系,平面的基本性质,属于中档题.

练习册系列答案
相关题目
在△ABC中,角A,B,C的对边分别为a,b,c,若a2-b2=
bc,且sinC=2
sinB,则A等于( )
| 3 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
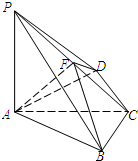 如图,四棱锥P-ABCD中,PA⊥底面ABCD,BC=CD=2,AC=4,∠ACB=∠ACD=60°,F为PC的中点,AF⊥PC.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,BC=CD=2,AC=4,∠ACB=∠ACD=60°,F为PC的中点,AF⊥PC.