题目内容
过抛物线y2=8x的焦点作倾斜角为
直线l,直线l与抛物线相交与A,B两点,则弦|AB|的长是 .
| π |
| 4 |
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:先设A、B两点的坐标,由抛物线的方程求出焦点坐标,再求出直线l的方程,联立直线方程和抛物线的方程消去y后,利用韦达定理求出x1+x2的值,代入焦点弦公式求解即可.
解答:
解:设A(x1,y1),B(x2,y2),
根据抛物线y2=8x方程得:焦点坐标F(2,0),
因为直线l倾斜角为
,所以直线l的方程是:y=x-2,
由
得,x2-12x+4=0,
则x1+x2=12,
所以弦|AB|=x1+x2+p=12+4=16,
故答案为:16.
根据抛物线y2=8x方程得:焦点坐标F(2,0),
因为直线l倾斜角为
| π |
| 4 |
由
|
则x1+x2=12,
所以弦|AB|=x1+x2+p=12+4=16,
故答案为:16.
点评:本题考查直线与抛物线相交所得焦点弦问题,以及一元二次方程根与系数的关系,体现了设而不求思想.

练习册系列答案
相关题目
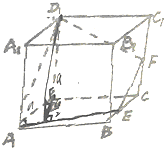 已知E、F分别为正方体ABCD-A1B1C1D1的棱BC,CC1的中点,设α为二面角D-AE-D1的平面角,求sinα=( )
已知E、F分别为正方体ABCD-A1B1C1D1的棱BC,CC1的中点,设α为二面角D-AE-D1的平面角,求sinα=( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知sinα+cosα=
,则sinα•cosα的值为( )
| 17 |
| 13 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
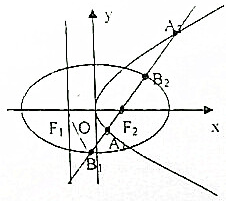 设抛物线C1:y2=4x的准线与x轴交于点F1,焦点为F2,以F1、F2为焦点,离心率为
设抛物线C1:y2=4x的准线与x轴交于点F1,焦点为F2,以F1、F2为焦点,离心率为 如图所示,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AB=2,BC=1,
如图所示,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AB=2,BC=1,