题目内容
若f(x)=sin(2ωx-
)的图象关于直线x=
对称,其中ω∈(-
,
).
(1)求f(x)的解析式;
(2)将y=f(x)的图象向左平移
个单位,再将得到的图象的横坐标变为原来的2倍(纵坐标不变)后得到y=g(x)的图象,求y=g(x)的解析式;
(3)若函数y=g(x)(x∈(
,3π))的图象与y=a的图象有三个交点且交点的横坐标成等比数列,求a的值.
| π |
| 6 |
| π |
| 3 |
| 1 |
| 2 |
| 5 |
| 2 |
(1)求f(x)的解析式;
(2)将y=f(x)的图象向左平移
| π |
| 3 |
(3)若函数y=g(x)(x∈(
| π |
| 2 |
考点:函数y=Asin(ωx+φ)的图象变换,数列的应用
专题:三角函数的图像与性质
分析:(1)由题意可得2ω•
-
=kπ+
(k∈Z),求得ω的值,可得函数f(x)的解析式.
(2)根据函数y=Asin(ωx+φ)的图象变换规律,可得函数g(x)的解析式.
(3)设函数g(x)的图象与y=a的图象有三个交点的横坐标为:(x1,a),(x2,a),(x3,a),且
<x1<x2<x3<3π.结合图象的对称性有
,解得x2=
,从而求得a的值.
| π |
| 3 |
| π |
| 6 |
| π |
| 2 |
(2)根据函数y=Asin(ωx+φ)的图象变换规律,可得函数g(x)的解析式.
(3)设函数g(x)的图象与y=a的图象有三个交点的横坐标为:(x1,a),(x2,a),(x3,a),且
| π |
| 2 |
|
| 4π |
| 3 |
解答:
解:(1)∵f(x)=sin(2ωx-
)的图象关于直线x=
对称,
∴2ω•
-
=kπ+
(k∈Z),
解得ω=
+1(k∈Z).
又∵ω∈(-
,
),
∴k=0,ω=1,
∴f(x)=sin(2x-
).
(2)将f(x)=sin(2x-
)的图象向左平移
个单位后,得到的图象的函数解析式为y=cos2x,
再将y=cos2x图象的横坐标变为原来的2倍后得到y=g(x)的图象,所以g(x)=cosx.
(3)设函数g(x)=cosx(x∈(
,3π))的图象与y=a的图象有三个交点的横坐标为:
(x1,a),(x2,a),(x3,a),且
<x1<x2<x3<3π.
则由已知,结合图象的对称性有
,解得x2=
,
∴a=cos
=-
.
| π |
| 6 |
| π |
| 3 |
∴2ω•
| π |
| 3 |
| π |
| 6 |
| π |
| 2 |
解得ω=
| 3k |
| 2 |
又∵ω∈(-
| 1 |
| 2 |
| 5 |
| 2 |
∴k=0,ω=1,
∴f(x)=sin(2x-
| π |
| 6 |
(2)将f(x)=sin(2x-
| π |
| 6 |
| π |
| 3 |
再将y=cos2x图象的横坐标变为原来的2倍后得到y=g(x)的图象,所以g(x)=cosx.
(3)设函数g(x)=cosx(x∈(
| π |
| 2 |
(x1,a),(x2,a),(x3,a),且
| π |
| 2 |
则由已知,结合图象的对称性有
|
| 4π |
| 3 |
∴a=cos
| 4π |
| 3 |
| 1 |
| 2 |
点评:本题主要考查由函数y=Asin(ωx+φ)的对称性,函数y=Asin(ωx+φ)的图象变换规律,属于中档题.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
若a=(
)2,b=x
,c=log
x,则当x>1时,a,b,c的大小关系是( )
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| A、a<b<c |
| B、c<b<a |
| C、c<a<b |
| D、a<c<b |
复数z=1+i3(i是虚数单位)的共轭复数所对应的点位于( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
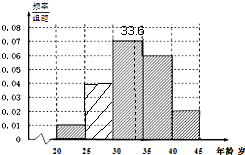 某市要对两千多名出租车司机的年龄进行调查,现从的频率分布直方图如图所示,利用这个残缺的频率分布直方图估计该市出租车司机年龄的中位数大约是( )
某市要对两千多名出租车司机的年龄进行调查,现从的频率分布直方图如图所示,利用这个残缺的频率分布直方图估计该市出租车司机年龄的中位数大约是( )| A、31.6岁 |
| B、32.6岁 |
| C、33.6岁 |
| D、36.6岁 |