题目内容
已知双曲线C的方程是:
-
=1(m≠0),若双曲线的离心率e>
,则实数m的取值范围是( )
| x2 |
| 2m-m2 |
| y2 |
| m |
| 2 |
| A、1<m<2. |
| B、m<0 |
| C、m<0或m>1 |
| D、m<0或1<m<2. |
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:分类讨论,结合双曲线的离心率e>
,建立不等式,即可求出实数m的取值范围.
| 2 |
解答:
解.由
⇒1<m<2,或
⇒m<0,
所以m<0或1<m<2.
故选:D.
|
|
所以m<0或1<m<2.
故选:D.
点评:本题考查双曲线的方程与离心率,考查分类讨论的数学思想,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
若U={1,2,3,4,5,6,7,8},A={1,2,3},B={5,6,7},则(∁UA)∩(∁UB)=( )
| A、{4,8} |
| B、{2,4,6,8} |
| C、{1,3,5,7} |
| D、{1,2,3,5,6,7} |
复数z=1+i3(i是虚数单位)的共轭复数所对应的点位于( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
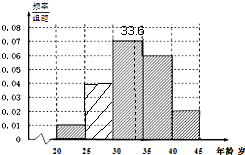 某市要对两千多名出租车司机的年龄进行调查,现从的频率分布直方图如图所示,利用这个残缺的频率分布直方图估计该市出租车司机年龄的中位数大约是( )
某市要对两千多名出租车司机的年龄进行调查,现从的频率分布直方图如图所示,利用这个残缺的频率分布直方图估计该市出租车司机年龄的中位数大约是( )| A、31.6岁 |
| B、32.6岁 |
| C、33.6岁 |
| D、36.6岁 |
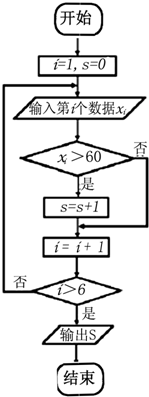 某学生一个学期的数学测试成绩一共记录了6个数据:x1=52,x2=70,x3=68,x4=55,x5=85,x6=90,执行如图所示的程序框图,那么输出的S是( )
某学生一个学期的数学测试成绩一共记录了6个数据:x1=52,x2=70,x3=68,x4=55,x5=85,x6=90,执行如图所示的程序框图,那么输出的S是( )