题目内容
若z=
=x+yi，x，y∈R，则集合{x，2x，y}子集个数是（ ）
| 2-i |
| 1+2i |
| A、8 | B、7 | C、6 | D、9 |
考点：复数相等的充要条件
专题：数系的扩充和复数
分析：利用复数的运算法则和集合的子集的意义即可得出．
解答：
解：∵z=
=x+yi，
∴x+yi=
=
=-i，
∴x=0，y=-1．
∴集合{x，2x，y}={0，1，-1}，其子集的个数为23，即为8．
故选：A．
| 2-i |
| 1+2i |
∴x+yi=
| (2-i)(1-2i) |
| (1+2i)(1-2i) |
| -5i |
| 5 |
∴x=0，y=-1．
∴集合{x，2x，y}={0，1，-1}，其子集的个数为23，即为8．
故选：A．
点评：本题考查了复数的运算法则和集合的子集的意义，属于基础题．
练习册系列答案
导学教程高中新课标系列答案
相关题目
若U={1，2，3，4，5，6，7，8}，A={1，2，3}，B={5，6，7}，则（∁UA）∩（∁UB）=（ ）
| A、{4，8} |
| B、{2，4，6，8} |
| C、{1，3，5，7} |
| D、{1，2，3，5，6，7} |
下列各组命题：
（1）p：a+b=2，q：直线x+y=0与圆（x-a）2+（y-b）2=2相切；
（2）p：|x|=x，q：x2+x≥0；
（3）设l，m均为直线，σ为平面，其中l?σ，m⊆σ，p：l∥σ，q：l∥m．
（4）p：数列log3n，log3（n+1），log3（n+3），（n∈N*）成等差数列；q：数列(
)n，
，3n（n∈N*）成等比数列．
其中，p是q的充分不必要条件的是（ ）
（1）p：a+b=2，q：直线x+y=0与圆（x-a）2+（y-b）2=2相切；
（2）p：|x|=x，q：x2+x≥0；
（3）设l，m均为直线，σ为平面，其中l?σ，m⊆σ，p：l∥σ，q：l∥m．
（4）p：数列log3n，log3（n+1），log3（n+3），（n∈N*）成等差数列；q：数列(
| 1 |
| 3 |
| 3 |
| 3n |
其中，p是q的充分不必要条件的是（ ）
| A、（1）（2） |
| B、（1）（4） |
| C、（1）（3） |
| D、（2）（3）（4） |
若a=(
)2，b=x
，c=log
x，则当x＞1时，a，b，c的大小关系是（ ）
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| A、a＜b＜c |
| B、c＜b＜a |
| C、c＜a＜b |
| D、a＜c＜b |
下列判断正确的是（ ）
| A、“正四棱锥的底面是正方形”的逆命题为真命题． | ||
| B、“ac2＞bc2”的充要条件是“a＞b”． | ||
C、不等式
| ||
| D、若“p或q”是真命题，则p，q中至少有一个真命题． |
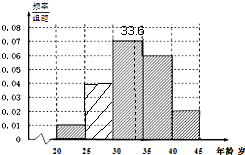某市要对两千多名出租车司机的年龄进行调查，现从的频率分布直方图如图所示，利用这个残缺的频率分布直方图估计该市出租车司机年龄的中位数大约是（ ）| A、31.6岁 |
| B、32.6岁 |
| C、33.6岁 |
| D、36.6岁 |