题目内容
若实数x，y满足：3x+4y=12，则x2+y2+2x的最小值是 ．
考点：直线与圆的位置关系
专题：直线与圆
分析：首先将x2+y2+2x变形为x2+y2+2x=[（x+1）2+y2]-1，通过点（x，y）与点（-1，0）之间的距离的最小值即可确定x2+y2+2x的最小值．
解答：
解：x2+y2+2x=[（x+1）2+y2]-1，
令z=[（x+1）2+y2，
则z即为点（x，y）与点（-1，0）之间的距离的平方．
∵点（-1，0）到直线3x+4y-12=0的距离为d=
=3，
∴zmin=32=9．
∴x2+y2+2x=[（x+1）2+y2]-1≥9-1=8．
∴x2+y2+2x的最小值是8．
故答案为：8．
令z=[（x+1）2+y2，
则z即为点（x，y）与点（-1，0）之间的距离的平方．
∵点（-1，0）到直线3x+4y-12=0的距离为d=
| |(-1)×3-12| |
| 5 |
∴zmin=32=9．
∴x2+y2+2x=[（x+1）2+y2]-1≥9-1=8．
∴x2+y2+2x的最小值是8．
故答案为：8．
点评：本题考查直线与圆的位置关系，利用点到直线的距离求最值等知识，属于中档题．
练习册系列答案
相关题目
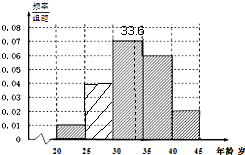某市要对两千多名出租车司机的年龄进行调查，现从的频率分布直方图如图所示，利用这个残缺的频率分布直方图估计该市出租车司机年龄的中位数大约是（ ）| A、31.6岁 |
| B、32.6岁 |
| C、33.6岁 |
| D、36.6岁 |