题目内容
3.已知函数f(x)=$\left\{\begin{array}{l}{{3}^{x}-3,x>0}\\{-{x}^{2}-4x-2,x≤0}\end{array}\right.$若函数g(x)=f(x)-2m有3个零点,则实数m的取值范围是( )| A. | [-1,1) | B. | (-1,1] | C. | (-2,2) | D. | (-1,1) |
分析 画出函数y=f(x)与函数y=2m的图象,求出两个函数有三个不同的交点时m的取值范围即可.
解答  解:函数g(x)=f(x)-2m有3个零点,
解:函数g(x)=f(x)-2m有3个零点,
即函数y=f(x)与函数y=2m的图象有三个不同的交点,
画出函数y=f(x)与函数y=2m的图象,如图所示;
观察函数的图象知,2m∈(-2,2),
解得m∈(-1,1).
故选:D.
点评 本题考查了利用函数的图象求函数零点的应用问题,是基础题目.

练习册系列答案
相关题目
14.已知集合A={1,2,3},B={x|(x-3)(x-6)=0},则A∩B等于( )
| A. | {1} | B. | {2,3} | C. | {3,6} | D. | {3} |
8.已知命题p:“?x∈R,x+1≥0”的否定是“?x∈R,x+1<0”;命题q:函数y=x-3是幂函数,则下列命题为真命题的是( )
| A. | p且q | B. | p或q | C. | ¬q | D. | p且(¬q) |
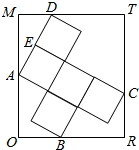 如图,矩形ORTM内放置5个边长均为$\sqrt{3}$的小正方形,其中A,B,C,D在矩形的边上,且E为AD的中点,则($\overrightarrow{AE}$-$\overrightarrow{BC}$)•$\overrightarrow{BD}$=-3.
如图,矩形ORTM内放置5个边长均为$\sqrt{3}$的小正方形,其中A,B,C,D在矩形的边上,且E为AD的中点,则($\overrightarrow{AE}$-$\overrightarrow{BC}$)•$\overrightarrow{BD}$=-3.