题目内容
12.若函数y=-x2+ax-2在区间(0,3]上既有最大值又有最小值,则实数a的取值范围为(0,3].分析 先求出函数的对称轴,根据二次函数的性质求出a的范围即可.
解答 解:函数y=-x2+ax-2,
对称轴x=$\frac{a}{2}$,
若函数在区间(0,3]上既有最大值又有最小值,
∴0<$\frac{a}{2}$≤$\frac{3}{2}$,解得:0<a≤3,
故答案为:(0,3].
点评 本题考查了二次函数的性质,考查函数的最值问题,是一道基础题.

练习册系列答案
相关题目
2.已知A(-1,1),B(3,1),C(1,3),则△ABC的BC边上的高所在的直线的方程为( )
| A. | x+y+2=0 | B. | x+y=0 | C. | x-y+2=0 | D. | x-y=0 |
3.已知函数f(x)=$\left\{\begin{array}{l}{{3}^{x}-3,x>0}\\{-{x}^{2}-4x-2,x≤0}\end{array}\right.$若函数g(x)=f(x)-2m有3个零点,则实数m的取值范围是( )
| A. | [-1,1) | B. | (-1,1] | C. | (-2,2) | D. | (-1,1) |
7.线段x-2y+1=0(-1≤x≤3)的垂直平分线方程为( )
| A. | x+2y-3=0 | B. | 2x+y-3=0 | C. | 2x+y-1=0 | D. | 2x-y-1=0 |
17.下列说法正确的是( )
| A. | 动物和植物的机体都是细胞组成的;植物细胞中有细胞核,所以动物细胞中也有细胞核.此推理是归纳推理 | |
| B. | “由圆的性质推出球的有关性质”是类比推理 | |
| C. | 观察下列各式:a+b=1,a2+b2=3,a3+b3=4,a4+b4=7,a5+b5=11,…则可得到a10+b10=122 | |
| D. | 函数f(x)是可导函数,已知f′(a)=0则a为f(x)的极值点 |
1.两个圆锥有公共底面,且两圆锥的顶点和底面圆周都在同一个球面上.若圆锥底面面积是球面面积的$\frac{3}{16}$,则这两个圆锥的体积之比为( )
| A. | 2:1 | B. | 5:2 | C. | 1:4 | D. | 3:1 |
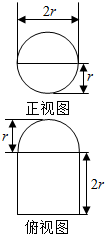 圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体三视图中的正视图和俯视图如图所示,若该几何体的表面积为4+5π,则半径r=1.
圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体三视图中的正视图和俯视图如图所示,若该几何体的表面积为4+5π,则半径r=1.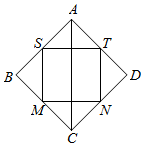 如图,记正方形ABCD四条边的中点为S、M、N、T,连接四个中点得小正方形SMNT.将正方形ABCD、正方形SMNT绕对角线AC旋转一周得到的两个旋转体的体积依次记为V1,V2,则V1:V2=( )
如图,记正方形ABCD四条边的中点为S、M、N、T,连接四个中点得小正方形SMNT.将正方形ABCD、正方形SMNT绕对角线AC旋转一周得到的两个旋转体的体积依次记为V1,V2,则V1:V2=( )