题目内容
15.在元旦联欢会上,某校的三个节目获得一致好评.其中哑剧表演有6人,街舞表演有12人,会唱有24人,现采用分层抽样的方法从这些学生中抽取7人进行采访.(1)求应从这三个节目中分别抽取的人数;
(2)若安排其中的A、B、C、D4人逐一作进一步的采访,求A、B2人不被连续采访的概率.
分析 (1)先求出三个节目的人数比,由此利用分层抽样的方法能求出应从这三个节目中分别抽取的人数.
(2)先求出基本事件总数,再求出A、B2人不被连续采访包含的基本事件个数,由此能求出A、B2人不被连续采访的概率.
解答 解:(1)∵三个节目的人数比为6:12:24,
用分层抽样的方法从这些学生中抽取7人,
则哑剧表演、街舞、合唱抽取的人数分别为1,2,4.
(2)安排其中的A、B、C、D4人逐一作进一步的采访,基本事件总数n=${A}_{4}^{4}$=24,
A、B2人不被连续采访包含的基本事件个数m=${A}_{2}^{2}{A}_{3}^{2}$=12,
∴A、B2人不被连续采访的概率p=$\frac{m}{n}$=$\frac{12}{24}$=$\frac{1}{2}$.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意分层抽样的性质的合理运用.

练习册系列答案
相关题目
3.已知函数f(x)=$\left\{\begin{array}{l}{{3}^{x}-3,x>0}\\{-{x}^{2}-4x-2,x≤0}\end{array}\right.$若函数g(x)=f(x)-2m有3个零点,则实数m的取值范围是( )
| A. | [-1,1) | B. | (-1,1] | C. | (-2,2) | D. | (-1,1) |
10.“a=-5”是“直线y=x+4与圆(x-a)2+(y-3)2=8相切”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
7.线段x-2y+1=0(-1≤x≤3)的垂直平分线方程为( )
| A. | x+2y-3=0 | B. | 2x+y-3=0 | C. | 2x+y-1=0 | D. | 2x-y-1=0 |
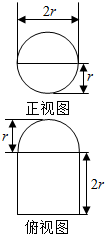 圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体三视图中的正视图和俯视图如图所示,若该几何体的表面积为4+5π,则半径r=1.
圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体三视图中的正视图和俯视图如图所示,若该几何体的表面积为4+5π,则半径r=1.