题目内容
13.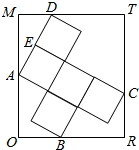 如图,矩形ORTM内放置5个边长均为$\sqrt{3}$的小正方形,其中A,B,C,D在矩形的边上,且E为AD的中点,则($\overrightarrow{AE}$-$\overrightarrow{BC}$)•$\overrightarrow{BD}$=-3.
如图,矩形ORTM内放置5个边长均为$\sqrt{3}$的小正方形,其中A,B,C,D在矩形的边上,且E为AD的中点,则($\overrightarrow{AE}$-$\overrightarrow{BC}$)•$\overrightarrow{BD}$=-3.
分析 以小正方形边的方向为坐标轴建立平面直角坐标系,求出各向量坐标,代入计算.
解答 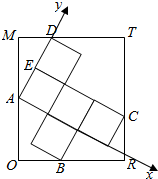 解:以A为坐标原点建立平面直角坐标系如图:
解:以A为坐标原点建立平面直角坐标系如图:
则A(0,0),E(0,$\sqrt{3}$),B(2$\sqrt{3}$,-$\sqrt{3}$),C(3$\sqrt{3}$,$\sqrt{3}$),D(0,2$\sqrt{3}$).
∴$\overrightarrow{AE}$=(0,$\sqrt{3}$),$\overrightarrow{BC}$=($\sqrt{3}$,2$\sqrt{3}$),$\overrightarrow{BD}$=(-2$\sqrt{3}$,3$\sqrt{3}$).
∴$\overrightarrow{AE}$-$\overrightarrow{BC}$=(-$\sqrt{3}$,-$\sqrt{3}$),
∴($\overrightarrow{AE}$-$\overrightarrow{BC}$)•$\overrightarrow{BD}$=6-9=-3.
故答案为-3.
点评 本题考查了平面向量的数量积运算,建立恰当的坐标系是解题关键.

练习册系列答案
相关题目
3.已知函数f(x)=$\left\{\begin{array}{l}{{3}^{x}-3,x>0}\\{-{x}^{2}-4x-2,x≤0}\end{array}\right.$若函数g(x)=f(x)-2m有3个零点,则实数m的取值范围是( )
| A. | [-1,1) | B. | (-1,1] | C. | (-2,2) | D. | (-1,1) |
1.两个圆锥有公共底面,且两圆锥的顶点和底面圆周都在同一个球面上.若圆锥底面面积是球面面积的$\frac{3}{16}$,则这两个圆锥的体积之比为( )
| A. | 2:1 | B. | 5:2 | C. | 1:4 | D. | 3:1 |
8.(log29)•(log34)等于( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | 4 |
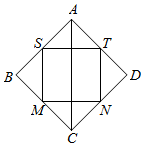 如图,记正方形ABCD四条边的中点为S、M、N、T,连接四个中点得小正方形SMNT.将正方形ABCD、正方形SMNT绕对角线AC旋转一周得到的两个旋转体的体积依次记为V1,V2,则V1:V2=( )
如图,记正方形ABCD四条边的中点为S、M、N、T,连接四个中点得小正方形SMNT.将正方形ABCD、正方形SMNT绕对角线AC旋转一周得到的两个旋转体的体积依次记为V1,V2,则V1:V2=( )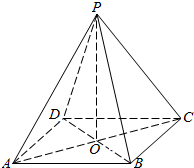 如图,O为正四棱锥P-ABCD的底面中心,该棱锥的侧棱长和底面边长都是2.试求:
如图,O为正四棱锥P-ABCD的底面中心,该棱锥的侧棱长和底面边长都是2.试求: