题目内容
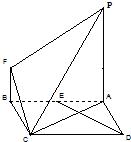 如图,正方形ABCD边长为2,PA⊥平面ABCD,BF∥PA,BF=
如图,正方形ABCD边长为2,PA⊥平面ABCD,BF∥PA,BF=| 1 |
| 3 |
(Ⅰ)求证:DE∥平面PCF;
(Ⅱ)若PC与平面ABCD所成的角为60°,求二面角F-PC-A的余弦值.
考点:二面角的平面角及求法,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(Ⅰ)根据线面平行的判定定理即可证明DE∥平面PCF;
(Ⅱ)建立坐标系,根据PC与平面ABCD所成的角为60°,利用向量法即可求二面角F-PC-A的余弦值.
(Ⅱ)建立坐标系,根据PC与平面ABCD所成的角为60°,利用向量法即可求二面角F-PC-A的余弦值.
解答:
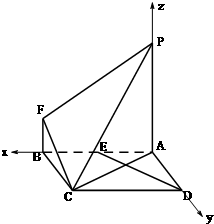 解:(Ⅰ)建系如图设A(0,0,0),B(2,0,0),
解:(Ⅰ)建系如图设A(0,0,0),B(2,0,0),
C(2,2,0),D(0,2,0),P(0,0,3m),F(2,0,m),
则E(1,0,0),
所以可计算得平面PCF的一个法向量为
=(2m,m,2),
=(1,-2,0),
即
•
=0,
所以DE∥平面PCF.
(Ⅱ)因为∠PCA为PC与平面ABCD所成的角,
即∠PCA=60°,
所以PA=2
,BF=
,m=
,
平面PAC中,
=(0,0,3m),
=(2,2,0),
平面PAC的一个法向量为
=(1,-1,0),
则cos<
,
>=
=
=
=
则二面角F-PC-A的余弦值为
.
 解:(Ⅰ)建系如图设A(0,0,0),B(2,0,0),
解:(Ⅰ)建系如图设A(0,0,0),B(2,0,0),C(2,2,0),D(0,2,0),P(0,0,3m),F(2,0,m),
则E(1,0,0),
所以可计算得平面PCF的一个法向量为
| n |
| DE |
即
| n |
| DE |
所以DE∥平面PCF.
(Ⅱ)因为∠PCA为PC与平面ABCD所成的角,
即∠PCA=60°,
所以PA=2
| 6 |
2
| ||
| 3 |
2
| ||
| 3 |
平面PAC中,
| AP |
| AC |
平面PAC的一个法向量为
| l |
则cos<
| n |
| l |
| ||||
|
|
| m | ||
5m2+4m•
|
| ||||||
|
| ||
| 13 |
则二面角F-PC-A的余弦值为
| ||
| 13 |
点评:本题主要考查空间直线和平面平行的判断,以及空间二面角的计算,利用向量法是解决本题的关键.

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
已知sinα+sinβ+sinγ=0,cosα+cosβ-cosγ=0,则cos(α-β)的值是( )
| A、-1 | ||
| B、1 | ||
C、-
| ||
D、
|
在Rt△ABC中,A=90°,AB=1,则
•
的值是( )
| AB |
| BC |
| A、1 |
| B、-1 |
| C、1或-1 |
| D、不确定,与B的大小,BC的长度有关 |
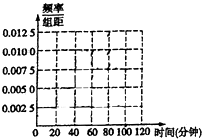 某中学为研究学生的身体素质与课外体育锻炼时间的关系,对400名高一学生的一周课外体育锻炼时间进行调查,结果如下表所示:
某中学为研究学生的身体素质与课外体育锻炼时间的关系,对400名高一学生的一周课外体育锻炼时间进行调查,结果如下表所示: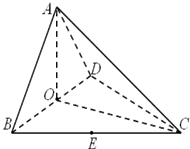 (Ⅰ)求证:AO⊥平面BCD;
(Ⅰ)求证:AO⊥平面BCD;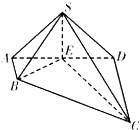 如图,四棱锥S-ABCD中,AB⊥AD,AB∥CD,CD=3AB=3,平面SAD⊥平面ABCD,E是线段AD上一点,AE=ED=
如图,四棱锥S-ABCD中,AB⊥AD,AB∥CD,CD=3AB=3,平面SAD⊥平面ABCD,E是线段AD上一点,AE=ED= 如图,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC.
如图,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC.