题目内容
如图,在四面体ABCD中,O是BD的中点,CA=CB=CD=BD=2,AB=AD=
.
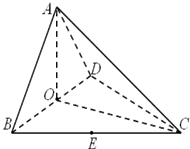 (Ⅰ)求证:AO⊥平面BCD;
(Ⅰ)求证:AO⊥平面BCD;
(Ⅱ)求二面角A-CD-B的正切值;
(Ⅲ)求点E到平面ACD的距离.
| 2 |
 (Ⅰ)求证:AO⊥平面BCD;
(Ⅰ)求证:AO⊥平面BCD;(Ⅱ)求二面角A-CD-B的正切值;
(Ⅲ)求点E到平面ACD的距离.
考点:二面角的平面角及求法,直线与平面垂直的判定,点、线、面间的距离计算
专题:空间位置关系与距离,空间角
分析:(Ⅰ)根据线面垂直的判定定理即可证明AO⊥平面BCD;
(Ⅱ)法1:求二面角A-CD-B的平面角,然后根据边角关系即可得到二面角的正切值;
法2:建立坐标系,求出法向量,利用向量法即可得到结论.
(Ⅲ)方法1:利用等积法求点E到平面ACD的距离.
方法2.利用向量法求距离.
(Ⅱ)法1:求二面角A-CD-B的平面角,然后根据边角关系即可得到二面角的正切值;
法2:建立坐标系,求出法向量,利用向量法即可得到结论.
(Ⅲ)方法1:利用等积法求点E到平面ACD的距离.
方法2.利用向量法求距离.
解答:
(Ⅰ)证明:连结OC,
∵BO=DO,AB=AD,∴AO⊥BD.
∵BO=DO,BC=CD,∴CO⊥BD.
在△AOC中,由已知可得AO=1,CO=
.
而AC=2,∴AO2+CO2=AC2,∴∠AOC=90°,
即AO⊥OC.
∵BD∩OC=O,∴AO⊥平面BCD,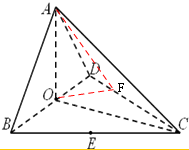
(Ⅱ)作OF⊥CD于F,连AF,
由(1)知,AO⊥CD,故CD⊥平面AOF,
∴CD⊥AF,∴∠AFO是二面角A-CD-B的平面角,
易知OF=
,∴tan∠AFO=
.
即所求二面角A-CD-B的正切值为
.
(Ⅲ)设点E到平面ACD的距离为h.
∵VE-ACD=VA-CDE,∴
h.S△ACD=
.AO.S△CDE.
在△ACD中,CA=CD=2,AD=
,
∴S△ACD=
×
×
=
.
而AO=1,S△CDE=
×
×22=
,
∴h=
=
=
.
∴点E到平面ACD的距离为
.
方法二:(Ⅰ)同方法一.
(Ⅱ)解:以O为原点,如图建立空间直角坐标系,则B(1,0,0),D(-1,0,0),
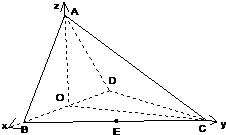 (Ⅲ)解:设平面ACD的法向量为
(Ⅲ)解:设平面ACD的法向量为
=(x,y,z),则
,
∴
令y=1,得
=(-
,1,
)是平面ACD的一个法向量,又
=(-
,
,0),
∴点E到平面ACD的距离h=
=
=
.
∵BO=DO,AB=AD,∴AO⊥BD.
∵BO=DO,BC=CD,∴CO⊥BD.
在△AOC中,由已知可得AO=1,CO=
| 3 |
而AC=2,∴AO2+CO2=AC2,∴∠AOC=90°,
即AO⊥OC.
∵BD∩OC=O,∴AO⊥平面BCD,

(Ⅱ)作OF⊥CD于F,连AF,
由(1)知,AO⊥CD,故CD⊥平面AOF,
∴CD⊥AF,∴∠AFO是二面角A-CD-B的平面角,
易知OF=
| ||
| 2 |
2
| ||
| 3 |
即所求二面角A-CD-B的正切值为
2
| ||
| 3 |
(Ⅲ)设点E到平面ACD的距离为h.
∵VE-ACD=VA-CDE,∴
| 1 |
| 3 |
| 1 |
| 3 |
在△ACD中,CA=CD=2,AD=
| 2 |
∴S△ACD=
| 1 |
| 2 |
| 2 |
22-(
|
| ||
| 2 |
而AO=1,S△CDE=
| 1 |
| 2 |
| ||
| 4 |
| ||
| 2 |
∴h=
| AO.S△CDE |
| S△ACD |
1×
| ||||
|
| ||
| 7 |
∴点E到平面ACD的距离为
| ||
| 7 |
方法二:(Ⅰ)同方法一.
(Ⅱ)解:以O为原点,如图建立空间直角坐标系,则B(1,0,0),D(-1,0,0),
 (Ⅲ)解:设平面ACD的法向量为
(Ⅲ)解:设平面ACD的法向量为| n |
|
∴
|
令y=1,得
| n |
| 3 |
| 3 |
| EC |
| 1 |
| 2 |
| ||
| 2 |
∴点E到平面ACD的距离h=
|
| ||||
|
|
| ||
|
| ||
| 7 |
点评:本题主要考查空间直线和平面垂直的判断,以及空间二面角和距离的计算,利用定义法或向量法是解决本题的关键.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
将正奇数按照如卞规律排列,则2015所在的列数为( )


| A、15 | B、16 | C、17 | D、18 |
sin
的值为( )
| 37π |
| 6 |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
 如图,正方形ABCD边长为2,PA⊥平面ABCD,BF∥PA,BF=
如图,正方形ABCD边长为2,PA⊥平面ABCD,BF∥PA,BF= 已知:如图AD,BC,AE分别是⊙O的三条切线,切点分别是D,E,F,AG是⊙O的一条割线,交⊙O于F,G两点,△ABC的周长2
已知:如图AD,BC,AE分别是⊙O的三条切线,切点分别是D,E,F,AG是⊙O的一条割线,交⊙O于F,G两点,△ABC的周长2