题目内容

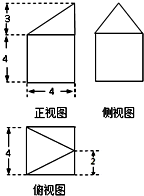
一个几何体的三视图如图所示，则此几何体的体积是（　　）
A、112B、80C、72D、64
考点：由三视图求面积、体积
专题：计算题,空间位置关系与距离
分析：由三视图可知此几何体是由一个棱柱和一个棱锥构成的组合体，代入数据分别求棱柱与棱锥的体积即可．
解答： 解：由三视图可知，此几何体是由一个棱柱和一个棱锥构成的组合体，
棱柱的体积为4×4×4=64；
棱锥的体积为
1
3
×4×4×3=16；
则此几何体的体积为80；
故选B．
点评：本题考查了三视图的识图与计算能力，属于基础题．
练习册系列答案
相关题目
函数f（x）=2sin（2x+
π
6
）的增区间为（　　）
A、[kπ-
π
12
，kπ+
5π
12
]，k∈Z
B、[kπ+
5π
12
，kπ+
11π
12
]，k∈Z
C、[kπ-
π
3
，kπ+
π
6
]，k∈Z
D、[kπ-
π
6
，kπ+
2π
3
]，k∈Z
已知函数f（x）满足：
①定义域为R；
②?x∈R，有f（x+2）=2f（x）；
③当x∈（0，2）时，f（x）=2-|2x-2|，设ρ（x）=f（x）-log2|x|（x∈（-8，0）∪（0，8））．
根据以上信息，可以得到函数ρ（x）的零点个数为
 
．
已知f（x）是定义在（-1，1）上的单调递减函数，且f（a-2）＜（1-a），求实数a的取值范围．
已知x、y∈R，且x2+y2=2，求x+y的取值范围．
若{an}为等差数列，Sn为其前n项和，若a1＞0，d＜0，S4=S10，则Sn＜0成立的最小的自然数n为
 
．
已知函数f（x）满足：f（1）=
1
4
，4f（x）f（y）=f（x+y）+f（x-y）（x∈R），则f（2013）=
 
．
某制造商为2008年北京奥运会生成一批直径为40mm的乒乓球，现随机抽取20只，测得每只球的直径（单位mm，保留两位小数）如下：
40.03　　40.00　　39.98　　40.00　　 39.99　　40.00　　39.98　　40.01　　39.98　　39.99　　　40.00　　39.99　　39.95　　40.0l　　　40.02　　39.98　　40.00　　39.99　　40.00　　39.96
（Ⅰ）完成下面的频率分布表，并画出频率分布直方图；
（Ⅱ）假定乒乓球的直径误差不超过0.02mm为合格品．若这批乒乓球的总数为10000只，试根据抽样检查结果估计这批产品的合格只数．

分　　　组		频数频率
频率
组距
[39.95，39.97）
[39.97，39.99）
[39.99，40.01）
[40.0l，40.03]
合计
如图，直角梯形ABCD中，AD∥BC，∠A=90°，AB=AD=3，DE⊥DC交AB于E，DF平分∠EDC交BC于F，连接EF．
（1）证明：FD平分∠EFC；
（2）当tan∠ADE=
1
3
时，求BF的长度．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网