题目内容
已知函数f(x)满足:
①定义域为R;
②?x∈R,有f(x+2)=2f(x);
③当x∈(0,2)时,f(x)=2-|2x-2|,设ρ(x)=f(x)-log2|x|(x∈(-8,0)∪(0,8)).
根据以上信息,可以得到函数ρ(x)的零点个数为 .
①定义域为R;
②?x∈R,有f(x+2)=2f(x);
③当x∈(0,2)时,f(x)=2-|2x-2|,设ρ(x)=f(x)-log2|x|(x∈(-8,0)∪(0,8)).
根据以上信息,可以得到函数ρ(x)的零点个数为
考点:函数零点的判定定理
专题:函数的性质及应用
分析:据条件:③当x∈[0,2]时,f(x)=2-|2x-2|可以作出函数图象位于[0,2]的拆线,再由?x∈R,有f(x+2)=2f(x),可将图象向右伸长,每向右两个单位长度,纵坐标变为原两倍,由此可以作出f(x)的图象,找出其与的交点,就可以得出ρ(x)的零点,问题迎刃而解.
解答:
 解:根据题意,作出函数y=f(x)(-8≤x≤8)的图象:
解:根据题意,作出函数y=f(x)(-8≤x≤8)的图象:
在同一坐标系里作出y=f(x)和y=log2|x|的图象,
可得两图象在有8个交点.所以有8个零点,
故答案为:8
 解:根据题意,作出函数y=f(x)(-8≤x≤8)的图象:
解:根据题意,作出函数y=f(x)(-8≤x≤8)的图象:在同一坐标系里作出y=f(x)和y=log2|x|的图象,
可得两图象在有8个交点.所以有8个零点,
故答案为:8
点评:本题考查函数零点个数的判断和数形结合思想的应用.在判断函数零点个数时,常转化为对应方程的根,利用根的个数来得结论或转化为对应两个函数的图象的交点,利用两个函数的图象的交点个数来判断.

练习册系列答案
相关题目
集合A={(x,y)|x∈R,y∈R},B=R,点(x,y)在映射f:A→B的作用下对应的数是
,则对于B中的数
,与之对应的A中的元素可能为( )
| y |
| 2x-y |
| 1 |
| 2 |
| A、(1,1) |
| B、(2,1) |
| C、(-2,-3) |
| D、(-3,-2) |
一个几何体的三视图如图所示,则此几何体的体积是( )
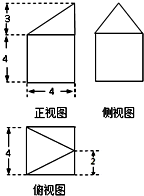

| A、112 | B、80 | C、72 | D、64 |