题目内容
已知f（x）是定义在（-1，1）上的单调递减函数，且f（a-2）＜（1-a），求实数a的取值范围．
考点：函数单调性的性质
专题：函数的性质及应用
分析：由题意可得
，化简求得a的范围．
|
解答：
解：由题意可得
，化简可得
，求得
＜a＜2．
|
|
| 3 |
| 2 |
点评：本题主要考查函数的单调性的性质，体现了等价转化的数学思想，属于基础题．
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
已知f（x）=x3-3x，g（x）=sinx+
cosx-m，若?x1∈[-1，3]，?x2∈[-
，
]，使得f（x1）＞g（x2），则实数m的取值范围是（ ）
| 3 |
| π |
| 6 |
| π |
| 3 |
| A、（3，+∞） |
| B、（-∞，3） |
| C、（-17，+∞） |
| D、（-∞，-3） |
一个几何体的三视图如图所示，则此几何体的体积是（ ）
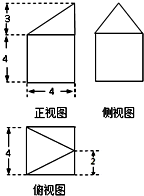
| A、112 | B、80 | C、72 | D、64 |