题目内容
已知函数f(x)满足:f(1)=
,4f(x)f(y)=f(x+y)+f(x-y)(x∈R),则f(2013)= .
| 1 |
| 4 |
考点:抽象函数及其应用
专题:计算题,函数的性质及应用
分析:令y=1,得到(x)=f(x+1)+f(x-1),将x换成x+1,得到f(x+1)=f(x+2)+f(x),即有f(x+2)+f(x-1)=0,再将x换成x+1,得到f(x)+f(x+3)=0.即f(x+6)=f(x).则函数的周期为6,则f(2013)=f(3),可令x=y=0,求出f(0),由f(x)+f(x+3)=0,令x=0,得f(3)=-
.即可得到答案.
| 1 |
| 2 |
解答:
解:当y=1,由4f(x)f(y)=f(x+y)+f(x-y)
可得4f(1)f(x)=f(x+1)+f(x-1),
即f(x)=f(x+1)+f(x-1),
f(x+1)=f(x+2)+f(x),即有f(x+2)+f(x-1)=0,
即有f(x)+f(x+3)=0.即f(x+6)=-f(x+3)=f(x).
则函数为周期T=6的函数,
则f(2013)=f(6×335+3)=f(3),
由于4f(x)f(y)=f(x+y)+f(x-y)
可令x=y=0,4f(0)f(0)=2f(0),则f(0)=
(0舍去).
由f(x)+f(x+3)=0,令x=0,得f(3)=-f(0)=-
.
故f(2013)=-
故答案为:-
.
可得4f(1)f(x)=f(x+1)+f(x-1),
即f(x)=f(x+1)+f(x-1),
f(x+1)=f(x+2)+f(x),即有f(x+2)+f(x-1)=0,
即有f(x)+f(x+3)=0.即f(x+6)=-f(x+3)=f(x).
则函数为周期T=6的函数,
则f(2013)=f(6×335+3)=f(3),
由于4f(x)f(y)=f(x+y)+f(x-y)
可令x=y=0,4f(0)f(0)=2f(0),则f(0)=
| 1 |
| 2 |
由f(x)+f(x+3)=0,令x=0,得f(3)=-f(0)=-
| 1 |
| 2 |
故f(2013)=-
| 1 |
| 2 |
故答案为:-
| 1 |
| 2 |
点评:本题考查抽象函数及运用,考查函数的周期性及运用,考查解决抽象函数的常用方法:赋值法,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
一个几何体的三视图如图所示,则此几何体的体积是( )
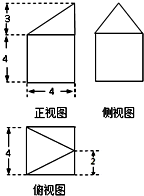

| A、112 | B、80 | C、72 | D、64 |
已知实数满足不等式组
,则2x-y的取值范围是( )
|
| A、[-1,3] |
| B、[-3,-1] |
| C、[-1,6] |
| D、[-6,1] |