题目内容
已知x、y∈R,且x2+y2=2,求x+y的取值范围.
考点:圆的参数方程
专题:坐标系和参数方程
分析:首先,根据已知条件,写出圆的参数方程
,然后,结合辅助角公式进行求解其范围即可.
|
解答:
解:∵x2+y2=2,
∴可设x=
cosα,
y=
sinα,
∴x+y=
(sinα+cosα)
=2sin(α+
)
∴x+y有最大值为2,最小值为-2,
∴x+y的取值范围[-2,2].
∴可设x=
| 2 |
y=
| 2 |
∴x+y=
| 2 |
=2sin(α+
| π |
| 4 |
∴x+y有最大值为2,最小值为-2,
∴x+y的取值范围[-2,2].
点评:本题重点考查了圆的参数方程、辅助角公式等知识,属于中档题,准确把握圆的参数方程是解题关键.

练习册系列答案
相关题目
一个几何体的三视图如图所示,则此几何体的体积是( )
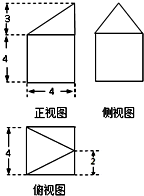

| A、112 | B、80 | C、72 | D、64 |