题目内容
在直角坐标系中,以坐标原点O为圆心的圆O与直线l:x-
y=8相切.
(1)求圆O的方程;
(2)圆O与x轴相交于A,B两点,圆内的动点P使PA,PO,PB成等比数列,求
•
的取值范围.
| 3 |
(1)求圆O的方程;
(2)圆O与x轴相交于A,B两点,圆内的动点P使PA,PO,PB成等比数列,求
| PA |
| PB |
考点:椭圆的简单性质
专题:等差数列与等比数列,平面向量及应用,直线与圆
分析:(1)求出圆心O到直线l的距离得圆的半径r,写出圆的方程即可;
(2)设出点P的坐标,求出A、B的坐标,由PA,PO,PB成等比数列,得出x、y的关系式,再求
•
的取值范围即可.
(2)设出点P的坐标,求出A、B的坐标,由PA,PO,PB成等比数列,得出x、y的关系式,再求
| PA |
| PB |
解答:
解:(1)∵圆心O到直线l:x-
y-8=0的距离是d=r,
∴r=
=4;
∴圆O的方程是x2+y2=16;
(2)设点P(x,y),其中x2+y2<16;
在圆O的方程x2+y2=16中,令y=0,得x=±4,
∴A(-4,0),B(4,0);
由PA,PO,PB成等比数列,
得PO2=PA•PB;
∴x2+y2=
,
化简得x2-y2=8;
由
,
得8≤x2<12;
∴
•
=x2+y2-16=2x2-24∈[-8,0).
| 3 |
∴r=
|1×0-
| ||||
|
∴圆O的方程是x2+y2=16;
(2)设点P(x,y),其中x2+y2<16;
在圆O的方程x2+y2=16中,令y=0,得x=±4,
∴A(-4,0),B(4,0);
由PA,PO,PB成等比数列,
得PO2=PA•PB;
∴x2+y2=
| ((x+4)2+y2)((x-4)2+y2) |
化简得x2-y2=8;
由
|
得8≤x2<12;
∴
| PA |
| PB |
点评:本题考查了直线与圆的应用问题,也考查了平面向量的应用问题,考查了等比中项的应用问题,是综合题目.

练习册系列答案
相关题目
函数f(x)=sin(2x+φ)(|φ<
|)的图象向左平移
个单位后关于原点对称,求函数f(x)在[0,
]上的最小值为( )
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
在正方体ABCD-A1B1C1D1中,E、F分别为AB、BC中点,则异面直线EF与AB1所成角的余弦值为( )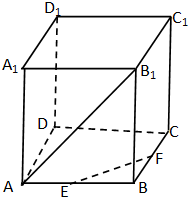

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知a,b为非零实数,若a>b且ab>0,则下列不等式成立的是( )
| A、a2>b2 | ||||
B、
| ||||
| C、ab2>a2b | ||||
D、
|