题目内容
给出下列命题:其中真命题的序号是: .
①若ab>0,a>b,则
<
;
②若a>|b|,则a2>b2;
③若a>b,c<d,则a-c>b-d;
④若a<b,m>0,则
<
.
①若ab>0,a>b,则
| 1 |
| a |
| 1 |
| b |
②若a>|b|,则a2>b2;
③若a>b,c<d,则a-c>b-d;
④若a<b,m>0,则
| a |
| b |
| a+m |
| b+m |
考点:命题的真假判断与应用
专题:简易逻辑
分析:直接利用不等式的性质逐一判断四个命题得答案.
解答:
解:对于①,若ab>0,a>b,两边同时乘以
得
<
,命题①正确;
对于②,若a>|b|,两边平方得a2>b2,命题②正确;
对于③,若a>b,c<d,则-d>-c,∴a-d>b-c,命题③错误;
④若a<b,m>0,取a=-5,b=-3,m=1,满足已知,但
<
不成立,命题④错误.
故答案为:①②.
| 1 |
| ab |
| 1 |
| a |
| 1 |
| b |
对于②,若a>|b|,两边平方得a2>b2,命题②正确;
对于③,若a>b,c<d,则-d>-c,∴a-d>b-c,命题③错误;
④若a<b,m>0,取a=-5,b=-3,m=1,满足已知,但
| a |
| b |
| a+m |
| b+m |
故答案为:①②.
点评:本题考查了命题的真假判断与应用,考查了不等式的性质,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知x>0,y>0,且
+
=1,若x+2y>m2+2m恒成立,则实数m的取值范围( )
| 2 |
| x |
| 1 |
| y |
| A、(-4,2) |
| B、(-1,2) |
| C、(1,2) |
| D、(-2,4) |
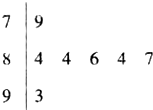 如图是2014年银川九中举行的校园之星评选活动中,七位评委为某位同学打出的分数的茎叶统计图,则数据的中位数和众数分别为( )
如图是2014年银川九中举行的校园之星评选活动中,七位评委为某位同学打出的分数的茎叶统计图,则数据的中位数和众数分别为( )| A、86,84 |
| B、84,84 |
| C、85,84 |
| D、85,93 |
(理科做) 定积分
(1-cosx)dx的值为( )
| ∫ | 2π 0 |
| A、2π | B、2π+1 |
| C、-2π | D、2π-1 |
若函数f(x)与函数g(x)=2x互为反函数,且f(a)+f(b)=4,则
+
的最小值为( )
| 1 |
| a |
| 1 |
| b |
| A、1 | ||
B、
| ||
C、
| ||
D、
|
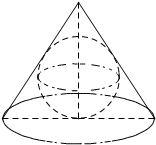 一个轴截面是等边三角形的圆锥(即该圆锥的母线长与底面直径相等)有一个内切球,设内切球的体积为V1,圆锥的体积为V2,则V1:V2=
一个轴截面是等边三角形的圆锥(即该圆锥的母线长与底面直径相等)有一个内切球,设内切球的体积为V1,圆锥的体积为V2,则V1:V2=