题目内容
已知不等式x2-5ax+b>0的解集为{x|x>4或x<1}
(1)求实数a,b的值;
(2)若0<x<1,f(x)=
+
,求f(x)的最小值.
(1)求实数a,b的值;
(2)若0<x<1,f(x)=
| a |
| x |
| b |
| 1-x |
考点:基本不等式,一元二次不等式的解法
专题:不等式的解法及应用
分析:(1)由三个二次的关系可得
,解方程组可得;
(2)由(1)知f(x)=
+
(
+
)[x+(1-x)]=5+
+
,由基本不等式可得.
|
(2)由(1)知f(x)=
| 1 |
| x |
| 4 |
| 1-x |
| 1 |
| x |
| 4 |
| 1-x |
| 1-x |
| x |
| 4x |
| 1-x |
解答:
解:(1)由题意可得
,解得
,
∴实数a,b的值分别为1,4;
(2)由(1)知f(x)=
+
∵0<x<1,∴0<1-x<1,∴
>0,
>0,
∴f(x)=
+
=(
+
)[x+(1-x)]
=5+
+
≥5+2
=9
当且仅当
=
即x=
时,等号成立.
∴f(x)的最小值为9.
|
|
∴实数a,b的值分别为1,4;
(2)由(1)知f(x)=
| 1 |
| x |
| 4 |
| 1-x |
∵0<x<1,∴0<1-x<1,∴
| 1 |
| x |
| 4 |
| 1-x |
∴f(x)=
| 1 |
| x |
| 4 |
| 1-x |
| 1 |
| x |
| 4 |
| 1-x |
=5+
| 1-x |
| x |
| 4x |
| 1-x |
|
当且仅当
| 1-x |
| x |
| 4x |
| 1-x |
| 1 |
| 3 |
∴f(x)的最小值为9.
点评:本题考查基本不等式,涉及一元二次不等式的解集,属基础题.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
数列{an}是各项均为正数的等比数列,公比q=3且a1a2a3…a30=330,则a3a6a9…a30=( )
| A、310 |
| B、315 |
| C、320 |
| D、325 |
抛物线y=-
x2的准线方程为( )
| 1 |
| 6 |
A、x=
| ||
B、y=
| ||
C、x=
| ||
D、y=
|
对任意两实数a、b,定义运算“*”如下:a*b=
,则函数f(x)=(log
x)*log2x的值域为( )
|
| 1 |
| 2 |
| A、(-∞,0) |
| B、(0,+∞) |
| C、(-∞,0] |
| D、[0,+∞) |
(理科做) 定积分
(1-cosx)dx的值为( )
| ∫ | 2π 0 |
| A、2π | B、2π+1 |
| C、-2π | D、2π-1 |
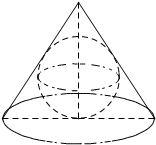 一个轴截面是等边三角形的圆锥(即该圆锥的母线长与底面直径相等)有一个内切球,设内切球的体积为V1,圆锥的体积为V2,则V1:V2=
一个轴截面是等边三角形的圆锥(即该圆锥的母线长与底面直径相等)有一个内切球,设内切球的体积为V1,圆锥的体积为V2,则V1:V2=