题目内容
设函数f(x)=x3+ax2-a2x+m(a>0)
(1)若a=1时函数f(x)有三个互不相同的零点,求实数m的取值范围;
(2)若对任意的a∈[3,6],x∈[-2,2],不等式f(x)≤1恒成立,求实数m的取值范围.
(1)若a=1时函数f(x)有三个互不相同的零点,求实数m的取值范围;
(2)若对任意的a∈[3,6],x∈[-2,2],不等式f(x)≤1恒成立,求实数m的取值范围.
考点:利用导数求闭区间上函数的最值,函数零点的判定定理
专题:计算题,函数的性质及应用,导数的综合应用
分析:(1)当a=1时,f(x)=x3+x2-x+m,化为m=-x3-x2+x有三个互不相同的实数根,求导确定单调性并求极值,由极值求实数m的取值范围;
(2)求导,确定函数f(x)=x3+ax2-a2x+m在[-2,2]上的最大值,不等式f(x)≤1恒成立可化为-8+4a+2a2+m≤1,从而求实数m的取值范围.
(2)求导,确定函数f(x)=x3+ax2-a2x+m在[-2,2]上的最大值,不等式f(x)≤1恒成立可化为-8+4a+2a2+m≤1,从而求实数m的取值范围.
解答:
解:(1)当a=1时,f(x)=x3+x2-x+m,
因为f(x)有三个互不相同的零点,所以f(x)=x3+x2-x+m=0,
即m=-x3-x2+x有三个互不相同的实数根,
令g(x)=-x3-x2+x,则g′(x)=-3x2-2x+1=-(3x-1)(x+1),
易知g(x)在(-∞,-1)和(
,+∞)上为减函数,在(-1,
)为增函数,
则g(x)的极小值:g(-1)=-1g(x)的极大值:g(
)=
,
则-1<m<
.
(2)∵f′(x)=3x2+2ax-a2=3(x-
)(x+a),且a>0,
∴函数f(x)的递减区间为(-a,
),递增区间为(-∞,-a)和(
,+∞);
当a∈[3,6]时,
∈[1,2],-a≤-3又x∈[-2,2],
∵f(-2)-f(2)=4a2-16>0,
∴fmax(x)=f(-2)=-8+4a+2a2+m,
又∵f(x)≤1在x∈[-2,2]上恒成立,
∴fmax(x)≤1,
即-8+4a+2a2+m≤1,
即m≤-2a2-4a+9在a∈[3,6]恒成立,
∴m≤-87.
因为f(x)有三个互不相同的零点,所以f(x)=x3+x2-x+m=0,
即m=-x3-x2+x有三个互不相同的实数根,
令g(x)=-x3-x2+x,则g′(x)=-3x2-2x+1=-(3x-1)(x+1),
易知g(x)在(-∞,-1)和(
| 1 |
| 3 |
| 1 |
| 3 |
则g(x)的极小值:g(-1)=-1g(x)的极大值:g(
| 1 |
| 3 |
| 5 |
| 27 |
则-1<m<
| 5 |
| 27 |
(2)∵f′(x)=3x2+2ax-a2=3(x-
| a |
| 3 |
∴函数f(x)的递减区间为(-a,
| a |
| 3 |
| a |
| 3 |
当a∈[3,6]时,
| a |
| 3 |
∵f(-2)-f(2)=4a2-16>0,
∴fmax(x)=f(-2)=-8+4a+2a2+m,
又∵f(x)≤1在x∈[-2,2]上恒成立,
∴fmax(x)≤1,
即-8+4a+2a2+m≤1,
即m≤-2a2-4a+9在a∈[3,6]恒成立,
∴m≤-87.
点评:本题考查了导数的综合应用,属于基础题.

练习册系列答案
相关题目
过点(-2,4)且在两坐标轴上截距的绝对值相等的直线有( )
| A、1条 | B、2条 | C、3条 | D、4条 |
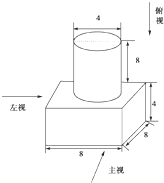 一几何体的直观图如图所示:
一几何体的直观图如图所示:



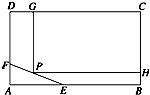 如图,长方形ABCD形状的空地,AB=100m,BC=80m,现决定在该空地上规划出一块矩形CGPH地面学生公寓,要求一边落在CD 上,但不得越过文物保护区△AEF的EF.△AEF的边AE=30m,AF=20m.
如图,长方形ABCD形状的空地,AB=100m,BC=80m,现决定在该空地上规划出一块矩形CGPH地面学生公寓,要求一边落在CD 上,但不得越过文物保护区△AEF的EF.△AEF的边AE=30m,AF=20m.
