题目内容
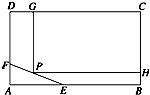如图，长方形ABCD形状的空地，AB=100m，BC=80m，现决定在该空地上规划出一块矩形CGPH地面学生公寓，要求一边落在CD 上，但不得越过文物保护区△AEF的EF．△AEF的边AE=30m，AF=20m．（1）要使矩形学生公寓CGPH的面积大于6000m2，CG的长度应在什么范围？
（2）长度CG和宽度CH分别为多少米时矩形学生公寓CGPH的面积最大？最大值是多少平方米？
考点：基本不等式在最值问题中的应用
专题：应用题,函数的性质及应用
分析：设CG=x，矩形CGPH面积为y，作EN⊥PH于点N，则
=
，EN=
，y=x-
=
-2x（760-2x）运用均值不等式求解最值．
| EN |
| 40 |
| x-140 |
| 60 |
| 2x-280 |
| 3 |
| 760-2x |
| 3 |
| 1 |
| 6 |
解答：
解 设CG=x，矩形CGPH面积为y，
作EN⊥PH于点N，则
=
，
EN=
∴HC=160-
=
≤
（
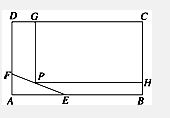
）2=
当2x=760-2x，x=190（m）即CG长为190m时，最大面积为
（m2）
作EN⊥PH于点N，则
| EN |
| 40 |
| x-140 |
| 60 |
EN=
| 2x-280 |
| 3 |
∴HC=160-
| 2x-280 |
| 3 |
| 760-2x |
| 3 |
≤
| 1 |
| 6 |
| 760 |
| 2 |
| 72200 |
| 3 |
当2x=760-2x，x=190（m）即CG长为190m时，最大面积为
| 72200 |
| 3 |
点评：本题考察了函数在实际问题中的应用，结合均值不等式求解．
练习册系列答案
口算小状元口算速算天天练系列答案
相关题目
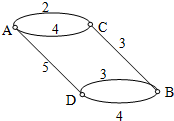如图，小圆圈表示网络的接点，接点之间的连接表示它们有网线相连．相连标注的数字表示该段网线单位时间内可以通过的最大信息量．现在从接点A向接点B传递信息，信息可以分开沿不同线路同时传递，则单位时间内从接点A向接点B传递的最大信息量为（ ）