题目内容
过点（-2，4）且在两坐标轴上截距的绝对值相等的直线有（ ）
| A、1条 | B、2条 | C、3条 | D、4条 |
考点：直线的图象特征与倾斜角、斜率的关系
专题：直线与圆
分析：根据直线截距的意义即可得到结论．
解答：
解：若直线过原点，则满足条件，此时设直线方程为y=kx，则4=-2k，解得k=-2，此时直线为y=-2x，
若直线不经过原点，则设直线的截距式方程为
+
=1，
∵直线过点（-2，4，），∴
+
=1，
∵|a|=|b|，
∴a=b或a=-b，
若a=b，则方程
+
=1等价为
+
=
=1，解得a=b=2，此时直线方程为x+y=2，
若a=-b，则方程
+
=1等价为
+
=
=1，解得b=6，a=-6，此时直线方程为x-y=-6，
故满足条件的直线有3条，
故选：C
若直线不经过原点，则设直线的截距式方程为
| x |
| a |
| y |
| b |
∵直线过点（-2，4，），∴
| -2 |
| a |
| 4 |
| b |
∵|a|=|b|，
∴a=b或a=-b，
若a=b，则方程
| -2 |
| a |
| 4 |
| b |
| -2 |
| a |
| 4 |
| a |
| 2 |
| a |
若a=-b，则方程
| -2 |
| a |
| 4 |
| b |
| -2 |
| -b |
| 4 |
| b |
| 6 |
| b |
故满足条件的直线有3条，
故选：C
点评：本题主要考查直线截距式方程的应用，注意要进行分类讨论．
练习册系列答案
相关题目
如图，四边形ABCD是正方形，MA⊥平面ABCD，MA∥PB，PB=AB=2MA=2．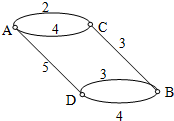
如图，小圆圈表示网络的接点，接点之间的连接表示它们有网线相连．相连标注的数字表示该段网线单位时间内可以通过的最大信息量．现在从接点A向接点B传递信息，信息可以分开沿不同线路同时传递，则单位时间内从接点A向接点B传递的最大信息量为（ ）