题目内容
已知函数f(x)=(
)|x|和g(x)=lg(2x+t)(t为常数).
(1)判断并证明f(x)的奇偶性;
(2)若x∈[0,1]时,g(x)有意义,求实数t的取值范围.
| 1 |
| 2 |
(1)判断并证明f(x)的奇偶性;
(2)若x∈[0,1]时,g(x)有意义,求实数t的取值范围.
考点:对数函数图象与性质的综合应用
专题:函数的性质及应用
分析:(1)f(x)是偶函数的定义式判断,(2)2x+t>0在[0,1]恒成立.即t>-2x,转化为函数最值求解.
解答:
解:(1)∵f(x)的定义域为R,
f(-x)=f(x),
∴f(x)是偶函数.
(2)∵x∈[0,1]时,g(x)有意义,
即2x+t在[0,1]大于0恒成立.
∴t>(-2x)max
∵y=-2x在[0,1]单调减
∴y=-2x的最大值为0
∴t>0
f(-x)=f(x),
∴f(x)是偶函数.
(2)∵x∈[0,1]时,g(x)有意义,
即2x+t在[0,1]大于0恒成立.
∴t>(-2x)max
∵y=-2x在[0,1]单调减
∴y=-2x的最大值为0
∴t>0
点评:本题考察了函数的性质,不等式的恒成立问题,构造函数的思想,有点综合性,但是难度不大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
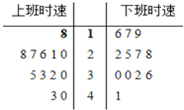 某市对上下班交通情况作抽样调查,作出上下班时间各抽取的12辆机动车行驶时速(单位:km/h)的茎叶图如图.则上、下班行驶时速的中位数分别为( )
某市对上下班交通情况作抽样调查,作出上下班时间各抽取的12辆机动车行驶时速(单位:km/h)的茎叶图如图.则上、下班行驶时速的中位数分别为( )| A、28与28.5 |
| B、29与28.5 |
| C、28与27.5 |
| D、29与27.5 |
如果a⊥b,那么a与b( )
| A、一定相交 | B、一定异面 |
| C、一定共面 | D、一定不平行 |