题目内容
已知数列{an}的通项公式为an=3n-50,若数列{an}的前n项和为Sn,
(1)求Sn;
(2)求Sn的最小值及相应n的值.
(1)求Sn;
(2)求Sn的最小值及相应n的值.
考点:等差数列的前n项和,等差数列的通项公式
专题:等差数列与等比数列
分析:(1)由已知得a1=3-50=-47,从而能求出Sn.
(2)由Sn=
n2-
n=
(n2-
n)=
(n-
)2-
,能求出Sn的最小值及相应n的值.
(2)由Sn=
| 3 |
| 2 |
| 97 |
| 2 |
| 3 |
| 2 |
| 97 |
| 3 |
| 3 |
| 2 |
| 97 |
| 6 |
| 9407 |
| 24 |
解答:
解:(1)∵数列{an}的通项公式为an=3n-50,
∴a1=3-50=-47,
Sn=
(-47+3n-50)=
n2-
n.
(2)Sn=
n2-
n=
(n2-
n)=
(n-
)2-
,
∴当n=16时,Sn的最小值为S16=
×
-
=-
.
∴a1=3-50=-47,
Sn=
| n |
| 2 |
| 3 |
| 2 |
| 97 |
| 2 |
(2)Sn=
| 3 |
| 2 |
| 97 |
| 2 |
| 3 |
| 2 |
| 97 |
| 3 |
| 3 |
| 2 |
| 97 |
| 6 |
| 9407 |
| 24 |
∴当n=16时,Sn的最小值为S16=
| 3 |
| 2 |
| 1 |
| 36 |
| 9407 |
| 24 |
| 4703 |
| 12 |
点评:本题考查数列的前n项和的求法,考查前n项和的最小值及相应的项数的求法,解题时要认真审题,是基础题.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
判定下列命题
①第一象限的角为锐角
②f(x)=xcosx为奇函数
③
-
=
④(
•
)•
=
•(
•
)
正确的为( )
①第一象限的角为锐角
②f(x)=xcosx为奇函数
③
| AB |
| AC |
| CB |
④(
| a |
| b |
| c |
| a |
| b |
| c |
正确的为( )
| A、①② | B、①③ | C、②③ | D、①④ |
在△ABC中,
=
,
=
,D为BC的中点,则
为( )
| AB |
| a |
| AC |
| b |
| AD |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
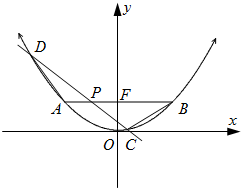 如图,已知抛物线M的参数方程为
如图,已知抛物线M的参数方程为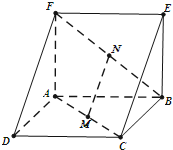 如图,三棱柱ADF-BCE中,除DF、CE外,其他的棱长均为2,AB⊥AF,平面ABCD⊥平面ABEF,M,N分别是AC,BF上的中点.
如图,三棱柱ADF-BCE中,除DF、CE外,其他的棱长均为2,AB⊥AF,平面ABCD⊥平面ABEF,M,N分别是AC,BF上的中点. 已知E、F、G、H分别是四面体ABCD的棱AD、CD、BD、BC的中点.求证:AH∥平面EFG.
已知E、F、G、H分别是四面体ABCD的棱AD、CD、BD、BC的中点.求证:AH∥平面EFG.