题目内容
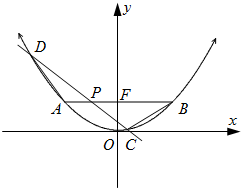 如图,已知抛物线M的参数方程为
如图,已知抛物线M的参数方程为
|
| 3 |
| 4 |
(1)请问
| |PC|•|PD| |
| |PA|•|PB| |
(2)若△APD和△BPC的面积相等,求点P的坐标.
考点:直线与圆锥曲线的关系
专题:计算题,圆锥曲线的定义、性质与方程
分析:(1)消参求出焦点坐标,进而确定A、B的坐标,设出直线的参数方程,联立利用韦达定理简化运算,
(2)由△APD和△BPC的面积相等,通过面积相等得到方程,解方程.
(2)由△APD和△BPC的面积相等,通过面积相等得到方程,解方程.
解答:
解:(1)消去参数s,得抛物线的方程为x2=2y,
∴F(0,
),
把y=
代入抛物线方程得A(-1,
),B(1,
),
于是设点P(x0,
)(-1<x0<1),
∵直线l的倾斜角为
π,
∴它的参数方程为
(其中t为参数),
代入抛物线方程得:(x0-
t)2=2(
+
t),
即t2-2
(x0+1)t+(2x02-2)=0,
设C,D对应的参数为tC,tD;
∴
(*),
∴
=
=
=2.
(2)∵△APD和△BPC的面积相等,
∴
|AP|•|PD|•sin∠APD=
|BP|•|PC|•sin∠BPC,
∴|AP|•|PD|=|BP|•|PC|,
又∵|AP|=x0-(-1)=x0+1,|BP|=1-x0,
∴|PC|=
|PD|,
∴tC=-
tD,
将其代入(*)式得
(1)2÷(2)得:
=2(x0-1)2,
∴(x0+1)2=x02,
∴x0=-
,
即点P的横坐标为-
,
∴点P的坐标为(-
,
).
∴F(0,
| 1 |
| 2 |
把y=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
于是设点P(x0,
| 1 |
| 2 |
∵直线l的倾斜角为
| 3 |
| 4 |
∴它的参数方程为
|
代入抛物线方程得:(x0-
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
即t2-2
| 2 |
设C,D对应的参数为tC,tD;
∴
|
∴
| |PC|•|PD| |
| |PA|•|PB| |
| |tC•tD| |
| (x0+1)(1-x0) |
| 2-2x02 |
| 1-x02 |
(2)∵△APD和△BPC的面积相等,
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴|AP|•|PD|=|BP|•|PC|,
又∵|AP|=x0-(-1)=x0+1,|BP|=1-x0,
∴|PC|=
| x0+1 |
| 1-x0 |
∴tC=-
| x0+1 |
| 1-x0 |
将其代入(*)式得
|
(1)2÷(2)得:
| 2(x02-1)2 |
| x02 |
∴(x0+1)2=x02,
∴x0=-
| 1 |
| 2 |
即点P的横坐标为-
| 1 |
| 2 |
∴点P的坐标为(-
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了抛物线的方程及参数方程的应用,化简是个难点,注意要细致,属于难题.

练习册系列答案
相关题目
设
是非零向量,λ是非零实数,下列结论中正确的是( )
| a |
A、
| ||||
B、|-λ
| ||||
C、
| ||||
D、|-λ
|
若a<b<0,则有( )
A、
| ||||
B、0<
| ||||
| C、b2>a2 | ||||
| D、|a|>-b |
将并排的有不同编号的5个房间安排给5个工作人员临时休息,假定每个人可以选择任一房间,且选择各个房间是等可能的,则恰有两个房间无人选择且这两个房间不相邻的安排方式的总数为( )
| A、900 | B、1500 |
| C、1800 | D、1440 |
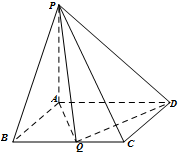 在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为矩形,AB=PA=tBC(t>0)
在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为矩形,AB=PA=tBC(t>0)