题目内容
已知一元二次不等式x2+ax+2a-3>0的解集为R
(1)若实数a的取值范围为集合A,求A.
(2)对任意的x∈A,都使得不等式x2+(b-1)x+9≥0恒成立.求b的取值范围.
(1)若实数a的取值范围为集合A,求A.
(2)对任意的x∈A,都使得不等式x2+(b-1)x+9≥0恒成立.求b的取值范围.
考点:二次函数的性质
专题:函数的性质及应用
分析:(1)利用一元二次不等式与二次函数的关系,得到x2+ax+2a-3>0的解集为R的等价条件为△<0;
(2)对任意的x∈A,都使得不等式x2+(b-1)x+9≥0恒成立,只要b≥1-(x+
),x∈(2,6)很成立,只要求出f(x)=1-(x+
),x∈(2,6)的最大值.
(2)对任意的x∈A,都使得不等式x2+(b-1)x+9≥0恒成立,只要b≥1-(x+
| 9 |
| x |
| 9 |
| x |
解答:
解:(1)因为x2+ax+2a-3>0的解集为R,所以△<0,即a2-8a+12<0,解得2<a<6,所以A={a|2<a<6}.
(2)对任意的x∈A,都使得不等式x2+(b-1)x+9≥0恒成立,只要b≥1-(x+
),x∈(2,6)很成立.
令f(x)=1-(x+
),x∈(2,6).∴f(x)≤1-2
=-5.当且仅当x=3时,3∈(2,6),取等号.
所以b≥-5.b的取值范围为:[-5,+∞).
(2)对任意的x∈A,都使得不等式x2+(b-1)x+9≥0恒成立,只要b≥1-(x+
| 9 |
| x |
令f(x)=1-(x+
| 9 |
| x |
x•
|
所以b≥-5.b的取值范围为:[-5,+∞).
点评:本题考查了一元二次不等式恒成立问题的解答方法;注意结合与二次函数的关系解答.

练习册系列答案
相关题目
若a<b<0,则有( )
A、
| ||||
B、0<
| ||||
| C、b2>a2 | ||||
| D、|a|>-b |
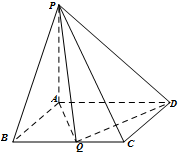 在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为矩形,AB=PA=tBC(t>0)
在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为矩形,AB=PA=tBC(t>0)