题目内容
(1)已知关于x的不等式|ax-1|+|ax-a|≥2(a>0),此不等式的解集为R,求实数a的取值范围.
(2)已知实数m,n,l,x,y,z满足m2+n2+l2=25,x2+y2+z2=36,mx+ny+lz=30,求表达式
的值.
(2)已知实数m,n,l,x,y,z满足m2+n2+l2=25,x2+y2+z2=36,mx+ny+lz=30,求表达式
| m+n+l |
| x+y+z |
考点:不等式的基本性质
专题:不等式的解法及应用
分析:(1)由于关于x的不等式|ax-1|+|ax-a|≥2(a>0),此不等式的解集为R,可得|ax-1|+|ax-a|≥
|ax-1+a-ax|=|a-1|≥2(a>0),解得a即可.
(2)利用“柯西不等式”即可得出.
|ax-1+a-ax|=|a-1|≥2(a>0),解得a即可.
(2)利用“柯西不等式”即可得出.
解答:
解:(1)∵关于x的不等式|ax-1|+|ax-a|≥2(a>0),此不等式的解集为R,
∴|ax-1|+|ax-a|≥|ax-1+a-ax|=|a-1|≥2(a>0),解得a≥3,∴实数a的取值范围是[3,+∞).
(2)∵m2+n2+l2=25,x2+y2+z2=36,mx+ny+lz=30,25×36=302,
(m2+n2+l2)(x2+y2+z2)≥(mx+ny+lz)2,
当且仅当
=
=
=
时上式成立.
∴
=
.
∴|ax-1|+|ax-a|≥|ax-1+a-ax|=|a-1|≥2(a>0),解得a≥3,∴实数a的取值范围是[3,+∞).
(2)∵m2+n2+l2=25,x2+y2+z2=36,mx+ny+lz=30,25×36=302,
(m2+n2+l2)(x2+y2+z2)≥(mx+ny+lz)2,
当且仅当
| m |
| x |
| n |
| y |
| l |
| z |
| 5 |
| 6 |
∴
| m+n+l |
| x+y+z |
| 5 |
| 6 |
点评:本题考查了含绝对值的三角不等式、柯西不等式的性质,考查了计算能力,属于中档题题.

练习册系列答案
相关题目
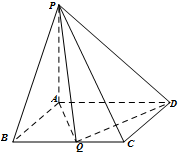 在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为矩形,AB=PA=tBC(t>0)
在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为矩形,AB=PA=tBC(t>0)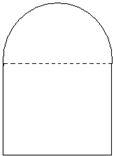 某建筑设计师设计如图所示的住宅窗户,用长度为p m的铝合金材料做窗框,怎样确定该窗户上半圆的半径和下半矩形的高,才能使窗户的透光,透气功能最好?
某建筑设计师设计如图所示的住宅窗户,用长度为p m的铝合金材料做窗框,怎样确定该窗户上半圆的半径和下半矩形的高,才能使窗户的透光,透气功能最好?