题目内容
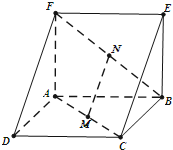 如图,三棱柱ADF-BCE中,除DF、CE外,其他的棱长均为2,AB⊥AF,平面ABCD⊥平面ABEF,M,N分别是AC,BF上的中点.
如图,三棱柱ADF-BCE中,除DF、CE外,其他的棱长均为2,AB⊥AF,平面ABCD⊥平面ABEF,M,N分别是AC,BF上的中点.(Ⅰ)求证:MN∥平面ADF;
(Ⅱ)求直线MN与平面ABCD所成角的大小.
考点:直线与平面所成的角,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(Ⅰ)取AB中点G,连接NG,MG,容易证明平面MNG∥平面ADF,所以MN∥平面ADF;
(Ⅱ)容易说明角NMG是直线MN与平面ABCD所成角,所以在Rt△MNG中,NG=MG=1,所以∠NMG=45°.
(Ⅱ)容易说明角NMG是直线MN与平面ABCD所成角,所以在Rt△MNG中,NG=MG=1,所以∠NMG=45°.
解答:
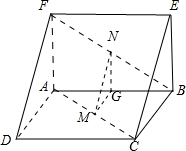 证明:(Ⅰ)如图,取AB中点G,连接MG,NG,∵N是BF中点,∴NG∥AF,且NG=
证明:(Ⅰ)如图,取AB中点G,连接MG,NG,∵N是BF中点,∴NG∥AF,且NG=
AF=1,AF?平面ADF,∴NG∥平面ADF;
同理可得MG∥平面ADF,NG∩MG=G,∴平面MNG∥平面ADF,MN?平面MNG,∴MN∥平面ADF;
(Ⅱ)∵平面ABCD⊥平面ABEF,平面ABCD∩平面ABEF=AB,AF⊥AB,AF?平面ABEF,∴AF⊥平面ABCD;
∵NG∥AF,∴NG⊥平面ABCD;
∴∠NMG是直线MN与平面ABCD所成角,由(Ⅰ)知MG=
BC=1,又NG=1,∴在Rt△MNG中,∠NMG=45°;
即直线MN与平面ABCD所成角的大小为45°.
 证明:(Ⅰ)如图,取AB中点G,连接MG,NG,∵N是BF中点,∴NG∥AF,且NG=
证明:(Ⅰ)如图,取AB中点G,连接MG,NG,∵N是BF中点,∴NG∥AF,且NG=| 1 |
| 2 |
同理可得MG∥平面ADF,NG∩MG=G,∴平面MNG∥平面ADF,MN?平面MNG,∴MN∥平面ADF;
(Ⅱ)∵平面ABCD⊥平面ABEF,平面ABCD∩平面ABEF=AB,AF⊥AB,AF?平面ABEF,∴AF⊥平面ABCD;
∵NG∥AF,∴NG⊥平面ABCD;
∴∠NMG是直线MN与平面ABCD所成角,由(Ⅰ)知MG=
| 1 |
| 2 |
即直线MN与平面ABCD所成角的大小为45°.
点评:考查线面平行的判定定理,面面平行的判定定理,面面平行的性质,线面角的定义及求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数y=e-x2+2x(0≤x<3)的值域是( )
| A、(e-3,1) |
| B、[e-3,1) |
| C、(e-3,e] |
| D、(1,e] |
如图,D为等腰三角形ABC底边AB的中点,则下列等式恒成立的是( )


A、
| ||||
B、
| ||||
C、
| ||||
D、
|
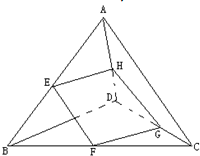 已知E、F、G、H分别是空间四边形四条边AB、BC、CD、DA的中点,BD⊥AC.求证:四边形EFGH是矩形.
已知E、F、G、H分别是空间四边形四条边AB、BC、CD、DA的中点,BD⊥AC.求证:四边形EFGH是矩形.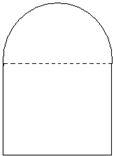 某建筑设计师设计如图所示的住宅窗户,用长度为p m的铝合金材料做窗框,怎样确定该窗户上半圆的半径和下半矩形的高,才能使窗户的透光,透气功能最好?
某建筑设计师设计如图所示的住宅窗户,用长度为p m的铝合金材料做窗框,怎样确定该窗户上半圆的半径和下半矩形的高,才能使窗户的透光,透气功能最好?