题目内容
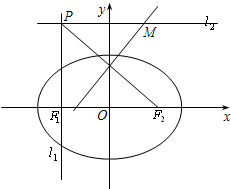 椭圆G:
椭圆G:| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
| 6 |
(1)求椭圆G的方程;
(2)求点M的轨迹E的曲线方程;
(3)点A,B为曲线E上异于原点O的两点,OA⊥OB,
| OA |
| OB |
| OC |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由题意可得:
,解得即可得出;
(2)点M满足:|MP|=|MF2|,由抛物线的定义可得:点M是以F2为焦点,l1为准线的抛物线,即可得出其轨迹E的方程.
(3)设直线OA,OB的方程分别为:y=kx,y=-
x.与抛物线方程联立解得A(
,
),同理可得B(4k2,-4k).可得S=|OA||OB|=
•
=16
,利用基本不等式的性质即可得出.
|
(2)点M满足:|MP|=|MF2|,由抛物线的定义可得:点M是以F2为焦点,l1为准线的抛物线,即可得出其轨迹E的方程.
(3)设直线OA,OB的方程分别为:y=kx,y=-
| 1 |
| k |
| 4 |
| k2 |
| 4 |
| k |
|
| 16k4+16k2 |
k2+
|
解答:
解:(1)由题意可得:
,
解得a2=3,c=1,b2=2.
∴椭圆G的方程为
+
=1.
(2)点M满足:|MP|=|MF2|,
∴点M是以F2为焦点,l1为准线的抛物线,
其轨迹E的方程为:y2=4x.
(3)设直线OA,OB的方程分别为:y=kx,y=-
x.(k≠0)
联立
,解得A(
,
),同理可得B(4k2,-4k).
∴S=|OA||OB|=
•
=16
≥32,当且仅当k=±1时取等号.
∴四边形AOBC的面积最小值为32.
|
解得a2=3,c=1,b2=2.
∴椭圆G的方程为
| x2 |
| 3 |
| y2 |
| 2 |
(2)点M满足:|MP|=|MF2|,
∴点M是以F2为焦点,l1为准线的抛物线,
其轨迹E的方程为:y2=4x.
(3)设直线OA,OB的方程分别为:y=kx,y=-
| 1 |
| k |
联立
|
| 4 |
| k2 |
| 4 |
| k |
∴S=|OA||OB|=
|
| 16k4+16k2 |
k2+
|
∴四边形AOBC的面积最小值为32.
点评:本题考查了椭圆与抛物线的定义标准方程及其性质、直线与抛物线交转化为方程联立、四边形的面积计算公式、基本不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
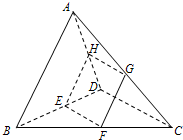 三棱锥A-BCD中,面ACD与面BCD均为正三角形,点E,F,G,H分别为BD,BC,AC,AD中点
三棱锥A-BCD中,面ACD与面BCD均为正三角形,点E,F,G,H分别为BD,BC,AC,AD中点