题目内容
下表提供了某厂生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据.
(Ⅰ)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程y=bx+a;
(Ⅱ)请求出相关指数R2,并说明解释变量对预报变量的贡献率为多少?
(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
(Ⅱ)请求出相关指数R2,并说明解释变量对预报变量的贡献率为多少?
(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)
考点:线性回归方程,相关系数
专题:概率与统计
分析:(Ⅰ)首先做出x,y的平均数,代入
,
的公式,利用最小二乘法做出线性回归直线的方程的系数,写出回归直线的方程,得到结果;(Ⅱ)直接根据相关指数公式进行求解即可.
 |
| a |
 |
| b |
解答:
解:(Ⅰ)∵由题意知
=
(3+4+5+6)=4.5,
=
(2..5+3+4+4.5)=0.7,
∴
=
=0.7,
=3.5-4.5×0.7=0.35,
∴线性回归方程是y=0.7x+0.35,
(Ⅱ)相关指数R2=1-
=1-
≈1-0.0013=0.9987,
∴解释变量对预报变量的贡献率为99.87%.
. |
| x |
| 1 |
| 4 |
. |
| y |
| 1 |
| 4 |
∴
 |
| b |
| 1.5×1+0.5×0.5+0.5×0.5+1.5×1 |
| 1.52+0.52+0.52+1.52 |
 |
| a |
∴线性回归方程是y=0.7x+0.35,
(Ⅱ)相关指数R2=1-
| |||||
|
=1-
| (2.5-2.45)2+(3-3.15)2+(4-3.85)2+(4.5-4.55)2 |
| (2.5-0.7)2+(3-0.7)2+(4-0.7)2+(4.5-0.7)2 |
≈1-0.0013=0.9987,
∴解释变量对预报变量的贡献率为99.87%.
点评:本题重点考查了线性回归直线方程及其求解,相关指数的计算等知识,属于中档题.考查运算求解能力.

练习册系列答案
相关题目
观察如图所示的四个几何体:(1)a是棱台;(2)b是圆台;(3)c是棱锥;(4)d不是棱柱.其中判断正确的是( )
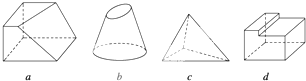

| A、(1)(2) | B、(3)(4) |
| C、(3) | D、(4) |
某商场实行优惠措施,若购物金额x在800元以上(含800元)打8折;若购物金额在500元以上(含500元)打9折,否则不打折.请设计一个算法程序框图,要求输入购物金额x,能输出实际交款额,并写出程序.
在球O表面上有A、B、C三个点,若∠AOB=∠BOC=∠COA=
,且O到平面的距离为2
,则此球的表面积为( )
| π |
| 3 |
| 2 |
| A、48π | B、36π |
| C、24π | D、12π |

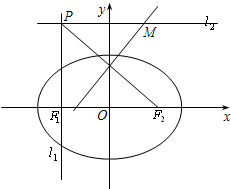 椭圆G:
椭圆G: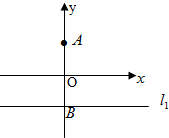 已知定点A(0,a)(a>0),直线l1:y=-a交y轴于点B,记过点A且与直线l1相切的圆的圆心为点C.
已知定点A(0,a)(a>0),直线l1:y=-a交y轴于点B,记过点A且与直线l1相切的圆的圆心为点C. 某海海岸线可以近似的看成直线,位于岸边A处 的海警发现海中B处有人求救,该海警没有直接从A处游向B处,而是沿岸边自A跑到距离B最近的D处,然后游向B处,若海警在岸边的行进速度是6米/秒,在海中的行进速度是2米/秒,(不考虑水流速度等因素)
某海海岸线可以近似的看成直线,位于岸边A处 的海警发现海中B处有人求救,该海警没有直接从A处游向B处,而是沿岸边自A跑到距离B最近的D处,然后游向B处,若海警在岸边的行进速度是6米/秒,在海中的行进速度是2米/秒,(不考虑水流速度等因素)