题目内容
设椭圆C:
+
=1(a>b>0)的离心率为
,左焦点到左准线的距离为1.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设直线l1:y=k(x-1)(k>0)交椭圆C于点A,B,且点A在第一象限内.直线l1与直线l2:x=6交于点D,直线l3:x=1与椭圆C在第一象限内交于点M.
(1)求点A,B的坐标(用k表示);
(2)求证:直线MA,MD,MB的斜率成等差数列.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)设直线l1:y=k(x-1)(k>0)交椭圆C于点A,B,且点A在第一象限内.直线l1与直线l2:x=6交于点D,直线l3:x=1与椭圆C在第一象限内交于点M.
(1)求点A,B的坐标(用k表示);
(2)求证:直线MA,MD,MB的斜率成等差数列.
考点:直线与圆锥曲线的综合问题
专题:等差数列与等比数列,圆锥曲线的定义、性质与方程
分析:(Ⅰ)根据椭圆C的离心率以及左焦点F到左准线的距离,求出a、c的值,再求出b2即可得出椭圆C的方程;
(Ⅱ)(1)由直线l1与椭圆C方程联立,求出方程组的解即可得A、B的坐标;
(2)由直线l3与椭圆C组成方程组,求出M的坐标,直线l1与直线l2组成方程组,求出D的坐标,计算直线MD、MA与MB的斜率值,判断直线MA、MD、MB的斜率是否成等差数列即可.
(Ⅱ)(1)由直线l1与椭圆C方程联立,求出方程组的解即可得A、B的坐标;
(2)由直线l3与椭圆C组成方程组,求出M的坐标,直线l1与直线l2组成方程组,求出D的坐标,计算直线MD、MA与MB的斜率值,判断直线MA、MD、MB的斜率是否成等差数列即可.
解答:
解:(Ⅰ)根据题意,椭圆C的离心率为e=
=
∴c=
a;
又∵左焦点F(-c,0)到左准线l:x=-
的距离为1,
∴-c+
=1,
即-
a+
=1,
解得a=
,
∴c=2,
∴b2=a2-c2=2;
∴椭圆C的方程为
+
=1;…(4分)
(Ⅱ)(1)根据题意,
由直线l1与椭圆C方程联立,得
,
解方程组,得A(
,
);
B(
,
);…(10分)
(2)由直线l3与椭圆C组成方程组
,
解得M(1,
);…(11分)
由直线l1与直线l2组成方程组
,
解得D(6,5k),
∴直线MD的斜率是kMD=
=k-
;…(12分)
直线MA的斜率是kMA=
=
;
直线MB的斜率是kMB=
=
;
∵kMA+kMB
=
=
=2k-
=2kMD;
∴直线MA、MD、MB的斜率成等差数列.…(16分)
| c |
| a |
| ||
| 3 |
∴c=
| ||
| 3 |
又∵左焦点F(-c,0)到左准线l:x=-
| a2 |
| c |
∴-c+
| a2 |
| c |
即-
| ||
| 3 |
| 3a | ||
|
解得a=
| 6 |
∴c=2,
∴b2=a2-c2=2;
∴椭圆C的方程为
| x2 |
| 6 |
| y2 |
| 2 |
(Ⅱ)(1)根据题意,
由直线l1与椭圆C方程联立,得
|
解方程组,得A(
3k2+
| ||
| 1+3k2 |
k(
| ||
| 1+3k2 |
B(
3k2-
| ||
| 1+3k2 |
-k(
| ||
| 1+3k2 |
(2)由直线l3与椭圆C组成方程组
|
解得M(1,
|
由直线l1与直线l2组成方程组
|
解得D(6,5k),
∴直线MD的斜率是kMD=
5k-
| ||||
| 6-1 |
| 1 | ||
|
直线MA的斜率是kMA=
| ||||||||
|
=
k(
| ||||||
|
直线MB的斜率是kMB=
| ||||||||
|
=
k(
| ||||||
|
∵kMA+kMB
=
[k(
| ||||||||||||||||
| 3(5k2+2)-1 |
=
-2
| ||||
| 15k2+5 |
=2k-
| 2 | ||
|
∴直线MA、MD、MB的斜率成等差数列.…(16分)
点评:本题考查了直线与圆锥曲线的综合应用问题,也考查了等差数列的应用问题,重点考查了计算能力,是较难的题目.

练习册系列答案
相关题目
观察如图所示的四个几何体:(1)a是棱台;(2)b是圆台;(3)c是棱锥;(4)d不是棱柱.其中判断正确的是( )
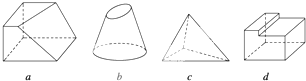

| A、(1)(2) | B、(3)(4) |
| C、(3) | D、(4) |
设P是椭圆
+
=1上一点,M、N分别是两圆:(x+4)2+y2=1和(x-4)2+y3=1上的点,则|PM|+|PN|的最小值、最大值的分别为( )
| x2 |
| 25 |
| y2 |
| 9 |
| A、9,12 | B、8,11 |
| C、8,12 | D、10,12 |
 椭圆G:
椭圆G: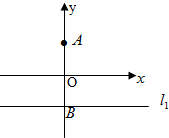 已知定点A(0,a)(a>0),直线l1:y=-a交y轴于点B,记过点A且与直线l1相切的圆的圆心为点C.
已知定点A(0,a)(a>0),直线l1:y=-a交y轴于点B,记过点A且与直线l1相切的圆的圆心为点C.