题目内容
某工厂产生的废气经过过滤后排放,过滤过程中废气的污染物数量Pmg/L与时间th间的关系为P=P0e-kt.如果在前5个小时消除了10%的污染物,试回答:
(1)10个小时后还剩百分之几的污染物?
(2)污染物减少50%需要花多少时间(精确到1h)?
(3)画出污染物数量关于时间变化的函数图象,并在图象上表示计算结果.
(1)10个小时后还剩百分之几的污染物?
(2)污染物减少50%需要花多少时间(精确到1h)?
(3)画出污染物数量关于时间变化的函数图象,并在图象上表示计算结果.
考点:函数的图象
专题:计算题,应用题,作图题,函数的性质及应用
分析:(1)由题意得P=P0e-5k=P0(1-10%);从而可得e-5k=90%;代入t=10即可;
(2)由题意得P0e-kt≤P050%;从而化简得0.9
≤
;从而解得;
(3)作函数图象确定.
(2)由题意得P0e-kt≤P050%;从而化简得0.9
| t |
| 5 |
| 1 |
| 2 |
(3)作函数图象确定.
解答:
解:(1)由题意得,
P=P0e-5k=P0(1-10%);
则e-5k=90%;
故当t=10时,
P=P0e-10k=P0(e-5k)2
=P0(90%)2
=P081%;
故10个小时后还剩81%的污染物;
(2)由题意,P0e-kt≤P050%;
即(e-5k)
≤
;
即0.9
≤
;
故t≥5log0.90.5≈33;
故污染物减少50%需要花33小时;
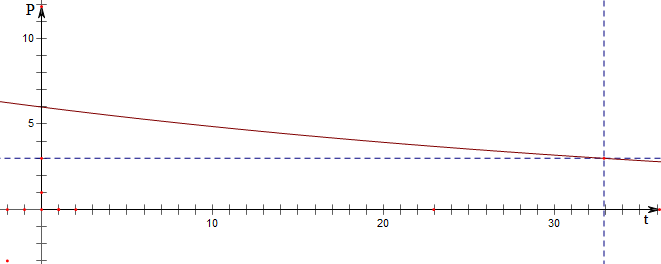
(3)作函数图象如下,
P=P0e-5k=P0(1-10%);
则e-5k=90%;
故当t=10时,
P=P0e-10k=P0(e-5k)2
=P0(90%)2
=P081%;
故10个小时后还剩81%的污染物;
(2)由题意,P0e-kt≤P050%;
即(e-5k)
| t |
| 5 |
| 1 |
| 2 |
即0.9
| t |
| 5 |
| 1 |
| 2 |
故t≥5log0.90.5≈33;
故污染物减少50%需要花33小时;
(3)作函数图象如下,

点评:本题考查了函数在实际问题中应用,同时考查了学生作图的能力,属于中档题.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
已知向量
=(2,1)和
=(x-1,y)垂直,则|
+
|的最小值为( )
| a |
| b |
| a |
| b |
A、
| ||
| B、5 | ||
C、2
| ||
D、
|
在△ABC中,a=5,b=8,C=60°,则
•
的值为( )
| CA |
| CB |
| A、-20 | ||
| B、20 | ||
C、20
| ||
D、-20
|