题目内容
给定两个命题:p:对任意实数x都有ax2+ax+1>0恒成立;q:关于x的方程x2-x+a=0有实数根,如果p和q中至少有一个为真命题,求实数a的取值范围.
考点:复合命题的真假
专题:简易逻辑
分析:根据二次函数恒成立的充要条件,我们可以求出命题p为真时,实数a的取值范围,根据二次函数有实根的充要条件,我们可以求出命题q为真时,实数a的取值范围,则命题p,q中一个为真,分类讨论后,即可得到实数a的取值范围.
解答:
解:对任意实数x都有ax2+ax+1>0恒成立?a=0或
?0≤a<4;
关于x的方程x2-x+a=0有实数根?△=1-4a≥0?a≤
;
p和q中至少有一个为真命题
如果p真q假,则有0≤a<4,且a>
,
∴
<a<4;
如果p假q真,则有a<0,或a≥4,且a≤
∴a<0;
如果p真q真,则有0≤a<4,且a≤
,
∴0≤a≤
;
所以实数a的取值范围为(-∞,4)
|
关于x的方程x2-x+a=0有实数根?△=1-4a≥0?a≤
| 1 |
| 4 |
p和q中至少有一个为真命题
如果p真q假,则有0≤a<4,且a>
| 1 |
| 4 |
∴
| 1 |
| 4 |
如果p假q真,则有a<0,或a≥4,且a≤
| 1 |
| 4 |
∴a<0;
如果p真q真,则有0≤a<4,且a≤
| 1 |
| 4 |
∴0≤a≤
| 1 |
| 4 |
所以实数a的取值范围为(-∞,4)
点评:本题考查的知识点是命题的真假判断与应用,复合命题的真假,函数恒成立问题,其中判断出命题p与命题q为真时,实数a的取值范围,是解答本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
数列{an},满足对任意的n∈N+,均有an+an+1+an+2为定值.若a7=2,a9=3,a98=4,则数列{an}的前100项的和S100=( )
| A、132 | B、299 |
| C、68 | D、99 |
按照程序框图执行,第三个输出的数是( )


| A、7 | B、6 | C、5 | D、4 |
曲线C1:y2=2px(p>0)的焦点F恰好是曲线C2:
-
=1(a>0,b>0)的右焦点,且曲线C1与曲线C2交点连线过点F,则曲线C2的离心率是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
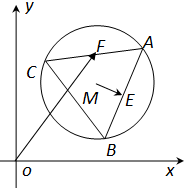 如图,已知圆M:(x-3)2+(y-3)2=4,△ABC为圆M的内接正三角形,E为边AB的中点,当正△ABC绕圆心M转动,且F是AC边上的中点,
如图,已知圆M:(x-3)2+(y-3)2=4,△ABC为圆M的内接正三角形,E为边AB的中点,当正△ABC绕圆心M转动,且F是AC边上的中点,