题目内容
对于一个有限数列p=(p1,p2,…,pn),p的蔡查罗和(蔡查罗是一位数学家)定义为
(S1+S2+…+Sn),其中Sk=p1+p2+…+pk(1≤k≤n,k∈N).若一个99项的数列(p1,p2,…,p99)的蔡查罗和为1000,那么100项数列(9,p1,p2,…,p99)的蔡查罗和为( )
| 1 |
| n |
| A、991 | B、992 |
| C、993 | D、999 |
考点:数列的求和
专题:等差数列与等比数列
分析:首先利用定义求出前99项的和,进一步求出结果.
解答:
解:由“蔡查罗和”定义,
{P1,P2,P99}的“蔡查罗和”为:
=1000
∴S1+S2+…+S99=99000,
则100项的数列{9,P1,P2,P99}“蔡查罗和”为:
=991.
故选B.
{P1,P2,P99}的“蔡查罗和”为:
| S1+S2+…+S99 |
| 99 |
∴S1+S2+…+S99=99000,
则100项的数列{9,P1,P2,P99}“蔡查罗和”为:
| 1+(1+S1)+…+(1+S99) |
| 100 |
故选B.
点评:本题考查的知识要点:利用信息求出结果,主要考查对知识的应用能力.属于基础题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
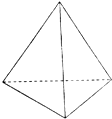
如图放置的六条棱长都相等的三棱锥,则这个几何体的侧视图是( )

| A、等腰三角形 |
| B、等边三角形 |
| C、直角三角形 |
| D、无两边相等的三角形 |
在△ABC中,“A>B”是“sinA>sinB”的( )
| A、充分必要条件 |
| B、充分非必要条件 |
| C、必要非充分条件 |
| D、非充分非必要条件 |
已知函数f(x)=ln
,则函数f(x)的图象( )
| 1+x |
| 1-x |
| A、关于x轴对称 |
| B、关于y轴对称 |
| C、关于原点对称 |
| D、关于直线y=x对称 |
已知等差数列{an}中,a3+a7-a10=0,a11-a4=4,记Sn=a1+a2+…+an,则S13=( )
| A、52 | B、56 | C、68 | D、78 |