题目内容
18.已知F1,F2为双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1(a>0,b>0)$的左、右焦点,过点F2作此双曲线一条渐近线的垂线,垂足为M,且满足|$\overrightarrow{M{F}_{1}}$|=3|$\overrightarrow{M{F}_{2}}$|,则此双曲线的离心率是( )| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{5}}{2}$ | C. | $\sqrt{5}$ | D. | $\frac{\sqrt{6}}{2}$ |
分析 由点到直线的距离公式可得|$\overrightarrow{M{F}_{2}}$|=b,则|$\overrightarrow{M{F}_{1}}$|=3b,cos∠F1OM=-$\frac{a}{c}$,由此利用余弦定理可得a,b的关系,进而得到a,c的关系,由离心率公式计算即可得到所求值.
解答 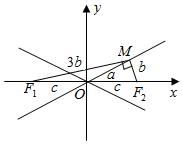 解:由F2(c,0)到渐近线y=$\frac{b}{a}$x的距离为d=$\frac{bc}{\sqrt{{a}^{2}+{b}^{2}}}$=b
解:由F2(c,0)到渐近线y=$\frac{b}{a}$x的距离为d=$\frac{bc}{\sqrt{{a}^{2}+{b}^{2}}}$=b
即有|$\overrightarrow{M{F}_{2}}$|=b,
则|$\overrightarrow{M{F}_{1}}$|=3b,在△MF1O中,|$\overrightarrow{OM}$|=a,|$\overrightarrow{O{F}_{1}}$|=c,
cos∠F1OM=-cos∠F2OM=-$\frac{a}{c}$,
由余弦定理可知$\frac{{a}^{2}+{c}^{2}-9{b}^{2}}{2ac}$=-$\frac{a}{c}$,
又c2=a2+b2,化简可得a2=2b2,
即有c2=a2+b2=$\frac{3}{2}$a2,
即有e=$\frac{c}{a}$=$\frac{\sqrt{6}}{2}$.
故选:D.
点评 本题考查双曲线的离心率的求法,解题时要认真审题,注意余弦定理的合理运用,考查运算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.设抛物线x2=2py的焦点与双曲线$\frac{y^2}{3}-{x^2}=1$的上焦点重合,则p的值为( )
| A. | $\sqrt{2}$ | B. | 4 | C. | 2$\sqrt{2}$ | D. | 8 |