题目内容
4．已知sinα=$\frac{4}{5}$，则$\frac{1+tanα}{1-tanα}$=-7或-$\frac{1}{7}$．分析 由已知利用同角三角函数基本关系式可求cosα的值，利用同角三角函数基本关系式即可化简求值得解．
解答 解：∵sinα=$\frac{4}{5}$，
∴cosα=±$\sqrt{1-si{n}^{2}α}$=±$\frac{3}{5}$，
∴$\frac{1+tanα}{1-tanα}$=$\frac{\frac{cosα+sinα}{cosα}}{\frac{cosα-sinα}{cosα}}$=$\frac{cosα+sinα}{cosα-sinα}$=-7或-$\frac{1}{7}$．
故答案为：-7或-$\frac{1}{7}$．
点评 本题主要考查了同角三角函数基本关系式在三角函数化简求值中的应用，属于基础题．
练习册系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
14．若圆C1：x2+y2+ax=0与圆C2：x2+y2+2ax+ytanθ=0都关于直线2x-y-1=0对称，则sinθcosθ=（ ）
| A． | $\frac{2}{5}$ | B． | -$\frac{6}{37}$ | C． | -$\frac{2}{5}$ | D． | -$\frac{2}{3}$ |
19．已知△ABC中，tanA=$\frac{cosB-cosC}{sinC-sinB}$成立，则△ABC为（ ）
| A． | 等腰三角形 | B． | A=60°的三角形 | ||
| C． | 等腰三角形或A=60°的三角形 | D． | 不能确定 |
9．如图所示的是函数y=2sin（ωx+φ）（|φ|＜$\frac{π}{2}$）的部分图象，那么（ ）
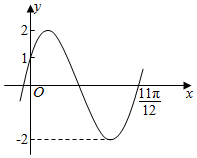
| A． | ω=$\frac{10}{11}$，φ=$\frac{π}{6}$ | B． | ω=$\frac{10}{11}$，φ=-$\frac{π}{6}$ | C． | ω=2，φ=$\frac{π}{6}$ | D． | ω=2，φ=-$\frac{π}{6}$ |
18．已知F1，F2为双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1（a＞0，b＞0）$的左、右焦点，过点F2作此双曲线一条渐近线的垂线，垂足为M，且满足|$\overrightarrow{M{F}_{1}}$|=3|$\overrightarrow{M{F}_{2}}$|，则此双曲线的离心率是（ ）
| A． | $\sqrt{2}$ | B． | $\frac{\sqrt{5}}{2}$ | C． | $\sqrt{5}$ | D． | $\frac{\sqrt{6}}{2}$ |