题目内容
6.设a,b,c是正实数,满足b+c≥a,则$\frac{b}{c}+\frac{c}{a+b}$的最小值为$\sqrt{2}-\frac{1}{2}$.分析 利用放缩法和基本不等式的性质进行求解.
解答 解:∵a,b,c是正实数,满足b+c≥a
∴$\frac{b}{c}+\frac{c}{a+b}$
≥$\frac{b}{c}$+$\frac{c}{2b+c}$
=$\frac{b}{c}$+$\frac{1}{\frac{2b}{c}+1}$
=$\frac{1}{2}$($\frac{2b}{c}+1)$+$\frac{1}{\frac{2b}{c}+1}$-$\frac{1}{2}$
$≥\sqrt{2}-\frac{1}{2}$(当且仅当b+c=a且$\frac{b}{c}=\frac{\sqrt{2}-1}{2}$时取等号)
故答案为:$\sqrt{2}-\frac{1}{2}$.
点评 本题主要考查基本不等式的应用和放缩法,属于中等题.

练习册系列答案
相关题目
11.已知两点A(-3,$\sqrt{3}$),B($\sqrt{3}$,-1),则直线AB的倾斜角θ等于( )
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{5}{6}π$ |
9.如图所示的是函数y=2sin(ωx+φ)(|φ|<$\frac{π}{2}$)的部分图象,那么( )
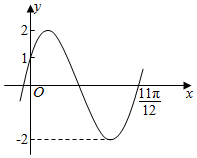

| A. | ω=$\frac{10}{11}$,φ=$\frac{π}{6}$ | B. | ω=$\frac{10}{11}$,φ=-$\frac{π}{6}$ | C. | ω=2,φ=$\frac{π}{6}$ | D. | ω=2,φ=-$\frac{π}{6}$ |
18.已知F1,F2为双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1(a>0,b>0)$的左、右焦点,过点F2作此双曲线一条渐近线的垂线,垂足为M,且满足|$\overrightarrow{M{F}_{1}}$|=3|$\overrightarrow{M{F}_{2}}$|,则此双曲线的离心率是( )
| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{5}}{2}$ | C. | $\sqrt{5}$ | D. | $\frac{\sqrt{6}}{2}$ |
15.一条光线沿直线2x-y+2=0照射到y轴后反射,则反射光线所在的直线方程为( )
| A. | 2x+y-2=0 | B. | 2x+y+2=0 | C. | x+2y+2=0 | D. | x+2y-2=0 |